RstatisTik/RstatisTikPortal/RcourSe/CourseOutline/RepeatedAov

Repeated Measures ANOVA (rma)

equivalent of the one-way ANOVA, but for related, not independent groups, \item in that sense it is the extension of the dependent t-test: he same people are being measured more than once on the same dependent variable
here we will look at the simplest design of rma

Statistical Model

remember in basic one-way Anova

$Y_{ij} = \mu + \alpha_j + Error_{ij}$

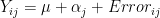
error was assumed to have variance of

$\sigma^2_{error}$

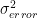
measurements and therefore the errors were independed

Statistical Model

in repeated measurement Anova

$Y_{ij} = \mu + time_j + S_j + (time\times S)_{ij} + Error_{ij}$

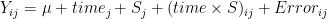
assumes still that errors have the same variances and
covariances are the same

Repeated Measures ANOVA (rma)

main hypothesis of rma:

$\mu_1=\mu_2=\ldots =\mu_n$

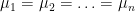
here we will look at the simplest design of rma
in this design the within group variance from above is splitted in variance caused by subject variability and the error variance

Repeated Measures ANOVA (rma)

So we have one more sum of sqares:

SS_Time
SS_within
SS_Subject
SS_error

Example

   1 > xx
   2 subject t1 t2 t3
   3 1       1 45 50 55
   4 2       2 42 42 45
   5 3       3 36 41 43
   6 4       4 39 35 40
   7 5       5 51 55 59
   8 6       6 44 49 56
   9 > n <- 6
  10 > k <- 3
  11 > require(reshape2)
  12 > xx <- melt(xx,id.vars = "subject")  
  13 > ## Sum of Squares time
  14 > (tmp <- aggregate(value ~ variable,FUN = "mean",data=xx))
  15 variable    value
  16 1       t1 42.83333
  17 2       t2 45.33333
  18 3       t3 49.66667
  19 > (sstime <- sum(6*(tmp$value - mean(xx$value))**2))
  20 [1] 143.4444
  21 > ## sum of squares within
  22 > (xx <- xx %>% group_by(variable) %>% mutate(gr.mean=mean(value)))
  23 subject variable value  gr.mean
  24 1        1       t1    45 42.83333
  25 2        2       t1    42 42.83333
  26 3        3       t1    36 42.83333
  27 4        4       t1    39 42.83333
  28 5        5       t1    51 42.83333
  29 6        6       t1    44 42.83333
  30 7        1       t2    50 45.33333
  31 8        2       t2    42 45.33333
  32 9        3       t2    41 45.33333
  33 10       4       t2    35 45.33333
  34 11       5       t2    55 45.33333
  35 12       6       t2    49 45.33333
  36 13       1       t3    55 49.66667
  37 14       2       t3    45 49.66667
  38 15       3       t3    43 49.66667
  39 16       4       t3    40 49.66667
  40 17       5       t3    59 49.66667
  41 18       6       t3    56 49.66667
  42 > (ssw <- sum((xx$value - xx$gr.mean)**2))
  43 [1] 715.5
  44 > ## sum of squares sub
  45 > (sub.xx <- xx %>% group_by(subject) %>% summarise(sub.mean=mean(value)))
  46 subject sub.mean
  47 1       1 50.00000
  48 2       2 43.00000
  49 3       3 40.00000
  50 4       4 38.00000
  51 5       5 55.00000
  52 6       6 49.66667
  53 > (sssub <- k*sum((sub.xx$sub.mean - mean(xx$value))**2))
  54 [1] 658.2778
  55 > ## sum of squares error
  56 > (sserror <- ssw - sssub)
  57 [1] 57.22222
  58 > ## ssw

Example

now it is ease to calculate the meas squares and the F statistic

   1 > ## mean squares
   2 > (mstime <- sstime/(k-1))
   3 [1] 71.72222
   4 > (mserror <- sserror/((n-1)*(k-1)))
   5 [1] 5.722222
   6 > (F <- mstime/mserror)
   7 [1] 12.53398
   8 > pf(F,k-1,((n-1)*(k-1)))
   9 [1] 0.9981144
  10 > 1-pf(F,k-1,((n-1)*(k-1)))
  11 [1] 0.001885591

Example

   1 > require(ez)
   2 > xx <- as.data.frame(xx)
   3 > (an <- ezANOVA(data=xx,dv = value,wid= subject, within = variable))
   4 Effect DFn DFd        F           p p<.05       ges
   5 2 variable   2  10 12.53398 0.001885591     * 0.1670008
   6 Effect         W         p p<.05
   7 2 variable 0.4335338 0.1879515      
   8 Effect       GGe       p[GG] p[GG]<.05      HFe       p[HF] p[HF]<.05
   9 2 variable 0.6383796 0.008985215         * 0.760165 0.005284458         *

MANOVA

in general, the framework of multivariate linear models extends quite elegantly to repeated-measure design
the p responses per individual related to the dependend variables in the model
the treatment sum of squares and the error sum of squares from the univariate case last week extends to the p x p sum of squares and crossproducts
test statistics (Wilks lambda, Pillai trace, Hotelling-Lawley trace, Roys maximum root) for testing are based on the non-zero latent roots of

$HE^{-1}$

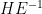
and attempt to capture how large H relative to E

all these statistics have transformations to F

MANOVA

the matrix H has the form

$\begin{displaymath} H = \begin{pmatrix} \mathrm{SSH}_{11} & \mathrm{SPH}_{12} & \cdots & \mathrm{SPH}_{1p} \\ \mathrm{SPH}_{12} & \mathrm{SSH}_{22} & \cdots & \mathrm{SPH}_{2p} \\ \vdots & \vdots & \ddots & \vdots \\ \mathrm{SPH}_{1p} & \mathrm{SPH}_{2p} & \cdots & \mathrm{SSH}_{pp} \\ \end{pmatrix} \end{displaymath}$

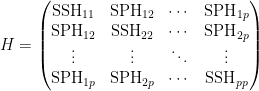
where e.g.

$\mathrm{SSH}_{22} = n \sum_{i=1}^k (\bar{y}_{i.2} - \bar{y}_{..2})^2$

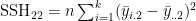
and e.g.

$\mathrm{SPH}_{12} = n \sum_{i=1}^k (\bar{y}_{i.1} - \bar{y}_{..1})(\bar{y}_{i.2} - \bar{y}_{..2})$

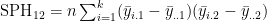
MANOVA

the matrix E has the form

\vdots & \vdots & \ddots & \vdots \\

where e.g.

$\mathrm{SSE}_{22} = \sum_{i=1}^k \sum_{j=1}^n (y_{ij2} - \bar{y}_{i.2})^2$

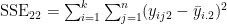
and e.g.

$\mathrm{SPE}_{12} = n \sum_{i=1}^k \sum_{j=1}^n (y_{ij1} - \bar{y}_{i.1})(y_{ij2} - \bar{y}_{i.2})$

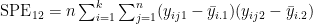
Example Data

weights of guinea pigs under three levels of vitamin E supplements
measured six times at the end of week 1, 3, 4, 5, 6, and 7
contained in guinea.rdata
Crowder and Hand 1990

Example Data

load the data print them on the screen

   1 > load("guinea.rdata")
   2 > head(guinea,10)
   3 Dose Animal  X1  X3  X4  X5  X6  X7
   4 1     0      1 455 460 510 504 436 466
   5 2     0      2 467 565 610 596 542 587
   6 3     0      3 445 530 580 597 582 619
   7 4     0      4 485 542 594 583 611 612
   8 5     0      5 480 500 550 528 562 576
   9 6     1      6 514 560 565 524 552 597
  10 7     1      7 440 480 536 484 567 569
  11 8     1      8 495 570 569 585 576 677
  12 9     1      9 520 590 610 637 671 702
  13 10    1     10 503 555 591 605 649 675

Example Data

reshape the data for ggplot2
plot boxplots and means per treatment group \scriptsize

   1 > require(reshape2)
   2 > dl <- melt(guinea,id.vars = c("Dose","Animal"))
   3 > dl$variable <- extract_numeric(dl$variable)
   4 > dl$group <- factor(dl$Dose)
   5 > head(dl)
   6 Dose Animal variable value group
   7 1    0      1        1   455     0
   8 2    0      2        1   467     0
   9 3    0      3        1   445     0
  10 4    0      4        1   485     0
  11 5    0      5        1   480     0
  12 6    1      6        1   514     1

Example Data

   1 > ggplot(dl,aes(x=variable,y=value,colour=group)) +
   2 +     geom_boxplot(aes(x=variable,group=factor(variable))) +
   3 +     stat_summary(fun.y="mean",geom = "line")

Basic multivariate model

design

\multicolumn{5}{c}{Factor A (Repeated Measures)} \\ \hline
\|Subjects \|A_1 \|A_2 \|\cdots \|A_p \|
\|S_{1} \|( y_{11} \|y_{12} \|\cdots \|y_{1p} ) \|= \mathbf{y^t_{1}}
\|S_{2} \|( y_{21} \|y_{22} \|\cdots \|y_{2p} ) \|= \mathbf{y^t_{2}}
\|S_{3} \|( y_{31} \|y_{32} \|\cdots \|y_{3p} ) \|= \mathbf{y^t_{3}}
\|\vdots \|\vdots \|\vdots \| \| \vdots o\| \vdots
\|S_{n} \|( y_{n1} \|y_{n2} \|\cdots \|y_{np} ) \|= \mathbf{y^t_{n}}

Basic multivariate model

basic MVLM with an intercept only
intercepts estimate the means at each instant of time

   1 > ## model
   2 > guinea$Dosef <- factor(guinea$Dose)
   3 > ### Basic multivariate linear model
   4 > mod <- lm(cbind(X1,X3,X4,X5,X6,X7) ~ 1,data=guinea)
   5 > (mod <- lm(cbind(X1,X3,X4,X5,X6,X7) ~ 1,data=guinea))
   6 X1     X3     X4     X5     X6     X7

Basic multivariate model

now test the Null hypothesis #!latex \mu_1=\mu_2=\ldots =\mu_n$
it is the simplest case of a multivariate test

   1 > (av <- Anova(mod))
   2 Type III MANOVA Tests: Pillai test statistic
   3 Df test stat approx F num Df den Df    Pr(>F)

extract the sum of squares and products matrix a) for hypothesis

   1 > av$SSP
   2 X1      X3      X4      X5      X6      X7
   3 X1 3545857 3901755 4188127 4133672 4224592 4471095
   4 X3 3901755 4293375 4608490 4548570 4648615 4919860
   5 X4 4188127 4608490 4946733 4882415 4989803 5280956
   6 X5 4133672 4548570 4882415 4818934 4924925 5212293
   7 X6 4224592 4648615 4989803 4924925 5033248 5326936
   8 X7 4471095 4919860 5280956 5212293 5326936 5637761

extract the sum of squares and products matrix b) for errors

   1 > av$SSPE
   2 X1    X3       X4      X5       X6       X7
   3 X1 11450.4 10716  5679.20  9326.6 13435.20 14389.80
   4 X3 10716.0 19668 13703.00 19888.0 21463.00 25693.00
   5 X4  5679.2 13703 13294.93 17357.8 18419.93 19089.73
   6 X5  9326.6 19888 17357.80 29166.4 27322.80 29977.20
   7 X6 13435.2 21463 18419.93 27322.8 45448.93 42336.73
   8 X7 14389.8 25693 19089.73 29977.2 42336.73 47268.93

size of the (degenerate) ellipse for the intercept term relative to that for Error gives the strength of evidence for the difference between the sample means and the means under
the H ellipse extends outside the E ellipse (anywhere), this signals that H0 is clearly rejected (for some linear combination of the response variables)

Testing within-S effects

but up to now there is no information about the within effect structure
for repeated measurement design we need to specify the intra-subject design
structure for within-S effects is specified through the arguments idata and idesign
we need to contruct a time variable for the different measurement times

   1 > idata <- data.frame(time=factor(c(1,3:7)))
   2 > (av2 <- Anova(mod, idata = idata, idesign = ~time))
   3 Type III Repeated Measures MANOVA Tests: Pillai test statistic
   4 Df test stat approx F num Df den Df    Pr(>F)    
   5 time         1   0.95566     43.1      5     10 1.899e-06 ***

Test Statistics

using the Wilks Statistic instead of the default (Pillai)

   1 > (av2 <- Anova(mod, test="Wilks", idata = idata, idesign = ~time))
   2 Type III Repeated Measures MANOVA Tests: Wilks test statistic
   3 Df test stat approx F num Df den Df    Pr(>F)    
   4 time         1  0.044335     43.1      5     10 1.899e-06 ***

The 4 Test Statistics

extract all test statistics

   1 > source("functions.r")
   2 > get.p.vals.all(av2)
   3 Df    test stat  approx F num Df den Df       Pr(>F)
   4 time Pillai         1 9.556647e-01   43.1108      5     10 1.899089e-06
   5 time Wilks          1 4.433528e-02   43.1108      5     10 1.899089e-06
   6 time HL             1 2.155540e+01   43.1108      5     10 1.899089e-06
   7 time Roy            1 2.155540e+01   43.1108      5     10 1.899089e-06

The 4 Test Statistics

when #!latex H_0 is true (i.e.

latex error! exitcode was 1 (signal 0), transscript follows:

This is pdfTeX, Version 3.14159265-2.6-1.40.19 (TeX Live 2019/dev/Debian) (preloaded format=latex)
entering extended mode
(./latex_bbe9a80d79364e057925f79143e8266b80751bcb_p.tex
LaTeX2e <2018-12-01>
(/usr/share/texlive/texmf-dist/tex/latex/base/article.cls
Document Class: article 2018/09/03 v1.4i Standard LaTeX document class
(/usr/share/texlive/texmf-dist/tex/latex/base/size12.clo))
(/usr/share/texlive/texmf-dist/tex/latex/amsfonts/amssymb.sty
(/usr/share/texlive/texmf-dist/tex/latex/amsfonts/amsfonts.sty))
(/usr/share/texlive/texmf-dist/tex/latex/amsmath/amsmath.sty
For additional information on amsmath, use the `?' option.
(/usr/share/texlive/texmf-dist/tex/latex/amsmath/amstext.sty
(/usr/share/texlive/texmf-dist/tex/latex/amsmath/amsgen.sty))
(/usr/share/texlive/texmf-dist/tex/latex/amsmath/amsbsy.sty)
(/usr/share/texlive/texmf-dist/tex/latex/amsmath/amsopn.sty))
(/usr/share/texlive/texmf-dist/tex/latex/amscls/amsthm.sty)
(/usr/share/texlive/texmf-dist/tex/latex/base/inputenc.sty)
No file latex_bbe9a80d79364e057925f79143e8266b80751bcb_p.aux.
! You can't use `macro parameter character #' in horizontal mode.
l.10    * when {{{#
                   !latex H_0
! Missing $ inserted.
<inserted text> 
                $
l.10    * when {{{#!latex H_
                            0
(/usr/share/texlive/texmf-dist/tex/latex/amsfonts/umsa.fd)
(/usr/share/texlive/texmf-dist/tex/latex/amsfonts/umsb.fd)
! Missing $ inserted.
<inserted text> 
                $
l.11 \end{document}
                   
[1] (./latex_bbe9a80d79364e057925f79143e8266b80751bcb_p.aux) )
(\end occurred inside a group at level 3)

### simple group (level 3) entered at line 10 ({)
### simple group (level 2) entered at line 10 ({)
### simple group (level 1) entered at line 10 ({)
### bottom level
(see the transcript file for additional information)
Output written on latex_bbe9a80d79364e057925f79143e8266b80751bcb_p.dvi (1 page,
 268 bytes).
Transcript written on latex_bbe9a80d79364e057925f79143e8266b80751bcb_p.log.

is false, the four tests have different probabilities of rejection

relative powers of the four tests depend on the configuration of the mean vectors in the #!latex s$-dimensional space, where {{{#!latex s=\min(p,\nu_H)
indication about this configuration is given by the eigenvalues of #!latex \mathbb{E}^{-1}\mathbb{H}

The 4 Test Statistics

   1 > source("functions.r")
   2 > get.p.vals.all(av2)
   3 Df    test stat  approx F num Df den Df       Pr(>F)
   4 time Pillai         1 9.556647e-01   43.1108      5     10 1.899089e-06
   5 time Wilks          1 4.433528e-02   43.1108      5     10 1.899089e-06
   6 time HL             1 2.155540e+01   43.1108      5     10 1.899089e-06
   7 time Roy            1 2.155540e+01   43.1108      5     10 1.899089e-06

The 4 Test Statistics

if one eigenvalue is large and the others are small (collinear mean vectors) Roy is the most powerful (in terms of power: Roy > LH > Wilk > Pillai)
intermediate between collinear and diffuse: Pillai > Wilk > LH > Roy
Pillai, Wilk, LH are robust against skewness
Pillai is better in presence of heterogeneity of covariance matrices
Pillai in most cases the best choice (but performs not well in case of collinearity)
Wilks not far behind but more sensible in case of severe heterogeneity of covariance matrices
nowadays software programs calculate all of them and most of the times they lead to the same conclusions, in case of conflicting conclusions examination of eigenvalues and covariance matrices is recommended

The 4 Test Statistics

calculate the eigenvalues

   1 > Re(eigen(solve(av$SSPE) %*% av$SSP[[1]])$values)
   2 [1]  8.941938e+02 -7.835860e-14 -7.835860e-14  2.256895e-13  2.256895e-13
   3 [6]  1.929296e-14
   4 > Re(eigen(solve(av2.mod2$SSPE$time) %*% av2.mod2$SSP$time)$values)
   5 [1]  2.476092e+01 -7.105427e-15 -1.958341e-15 -1.958341e-15  2.272995e-17

Add between-S effects

now add the group term to the model (Dosef)
design:

Add between-S effects

design:

\multicolumn{5}{c}{Factor A (Repeated Measures)} \\ \hline
Factor B \|Subjects \|A_1 \|A_2 \|\cdots \|A_p \|
B_1 \|S_{11} \|( y_{111} \|y_{112} \|\cdots \|y_{11p} ) \|= \mathbf{y^t_{11}}
\|S_{12} \|( y_{121} \|y_{122} \|\cdots \|y_{12p} ) \|= \mathbf{y^t_{12}}
\|S_{13} \|( y_{131} \|y_{132} \|\cdots \|y_{13p} ) \|= \mathbf{y^t_{13}}
\|\vdots \|\vdots \|\vdots \| \| \vdots \| \vdots
\|S_{1n} \|( y_{2n1} \|y_{2n2} \|\cdots \|y_{2np} ) \|= \mathbf{y^t_{2n}}
B_2 \|S_{21} \|( y_{211} \|y_{212} \|\cdots \|y_{21p} ) \|= \mathbf{y^t_{21}}
\|S_{22} \|( y_{221} \|y_{222} \|\cdots \|y_{22p} ) \|= \mathbf{y^t_{22}}
\|S_{23} \|( y_{231} \|y_{232} \|\cdots \|y_{23p} ) \|= \mathbf{y^t_{23}}
\|\vdots \|\vdots \|\vdots \| \| \vdots o\| \vdots
\|S_{2n} \|( y_{2n1} \|y_{2n2} \|\cdots \|y_{2np} ) \|= \mathbf{y^t_{2n}}
B_k \|S_{k1} \|( y_{k11} \|y_{k12} \|\cdots \|y_{k1p} ) \|= \mathbf{y^t_{k1}}
\|S_{k2} \|( y_{k21} \|y_{k22} \|\cdots \|y_{k2p} ) \|= \mathbf{y^t_{k2}}
\|S_{k3} \|( y_{k31} \|y_{k32} \|\cdots \|y_{k3p} ) \|= \mathbf{y^t_{k3}}
\|\vdots \|\vdots \|\vdots \| \| \vdots \| \vdots
\|S_{kn} \|( y_{kn1} \|y_{kn2} \|\cdots \|y_{knp} ) \|= \mathbf{y^t_{kn}}

Add between-S effects

   1 > (mod2 <- lm(cbind(X1,X3,X4,X5,X6,X7) ~ Dosef,data=guinea))
   2 X1     X3     X4     X5     X6     X7   
   3 Dosef1        28.0   31.6    5.4    5.4   56.4   72.0
   4 Dosef2        31.4   15.2   11.0   10.2   41.6   51.2
   5 > idata <- data.frame(time)
   6 > (av2.mod2 <- Anova(mod2, idata = idata, idesign = ~time))
   7 Type II Repeated Measures MANOVA Tests: Pillai test statistic
   8 Df test stat approx F num Df den Df    Pr(>F)    
   9 Dosef        2   0.14960      1.1      2     12   0.37821    
  10 time         1   0.96118     39.6      5      8 1.954e-05 ***

MANOVA Tests

   1 > get.p.vals.all(av2.mod2)
   2 Df    test stat    approx F num Df den Df       Pr(>F)
   3 Dosef Pillai        2 1.496026e-01    1.055525      2     12 3.782088e-01
   4 Dosef Wilks         2 8.503974e-01    1.055525      2     12 3.782088e-01
   5 Dosef HL            2 1.759208e-01    1.055525      2     12 3.782088e-01
   6 Dosef Roy           2 1.759208e-01    1.055525      2     12 3.782088e-01
   7 time Pillai         1 9.611815e-01   39.617478      5      8 1.954259e-05
   8 time Wilks          1 3.881848e-02   39.617478      5      8 1.954259e-05
   9 time HL             1 2.476092e+01   39.617478      5      8 1.954259e-05
  10 time Roy            1 2.476092e+01   39.617478      5      8 1.954259e-05

Assumptions MANOVA

Normal Distribution: The dependent variable should be normally distributed within groups. Overall, the F test is robust to non-normality, if the non-normality is caused by skewness rather than by outliers.
Linearity: MANOVA assumes that there are linear relationships among all pairs of dependent variables, all pairs of covariates, and all dependent variable-covariate pairs in each cell. Therefore, when the relationship deviates from linearity, the power of the analysis will be compromised.
Remember that the error variance is computed (SS error) by adding up the sums of squares within each group. If the variances in the two groups are different from each other, then adding the two together is not appropriate, and will not yield an estimate of the common within-group variance. Homoscedasticity can be examined graphically or by means of a number of statistical tests.
Homogeneity of Variances and Covariances: In multivariate designs, with multiple dependent measures, the homogeneity of variances assumption described earlier also applies. However, since there are multiple dependent variables, it is also required that their intercorrelations (covariances) are homogeneous across the cells of the design. There are various specific tests of this assumption.
Outliers: Like ANOVA, MANOVA is extremely sensitive to outliers. Outliers may produce either a Type I or Type II error and give no indication as to which type of error is occurring in the analysis. There are several programs available to test for univariate and multivariate outliers.
Multicollinearity and Singularity: When there is high correlation between dependent variables, one dependent variable becomes a near-linear combination of the other dependent variables. Under such circumstances, it would become statistically redundant and suspect to include both combinations.

Alternative Approach - Mixed Model

the mixed model looks very similar to ANOVA: #!latex Y_{ij} = \mu + \alpha_j + S_i + Error_{ij}$
the difference is the assumption:
- #!latex \mu is a fixed effect: no estimate of variability
- #!latex \alpha_j are also fixed effects: no estimate of variability
- #!latex S_i are random effects have normal distribution with zero mean
- #!latex E_{ij} are normally distributed with mean zero (as usual)

Alternative Approach - Mixed Model

this also can be written as follows:

#!latex Y_{ij} = [\pi_{0i} + \pi_{2i} \cdot \mathrm{TIME}_{ij}] + [\epsilon_{ij}] (structural part + stochastic part)
#!latex Y_{ij} is the value of subject #!latex i at time #!latex j as a linear function of #!latex \mathrm{TIME}

#!latex \pi_{0i} and #!latex \pi_{2i} are individual parameters that characterize its shape for the

latex error! exitcode was 1 (signal 0), transscript follows:

This is pdfTeX, Version 3.14159265-2.6-1.40.19 (TeX Live 2019/dev/Debian) (preloaded format=latex)
entering extended mode
(./latex_00683f2d325b5e274d8b6f04699fec10646ec9c7_p.tex
LaTeX2e <2018-12-01>
(/usr/share/texlive/texmf-dist/tex/latex/base/article.cls
Document Class: article 2018/09/03 v1.4i Standard LaTeX document class
(/usr/share/texlive/texmf-dist/tex/latex/base/size12.clo))
(/usr/share/texlive/texmf-dist/tex/latex/amsfonts/amssymb.sty
(/usr/share/texlive/texmf-dist/tex/latex/amsfonts/amsfonts.sty))
(/usr/share/texlive/texmf-dist/tex/latex/amsmath/amsmath.sty
For additional information on amsmath, use the `?' option.
(/usr/share/texlive/texmf-dist/tex/latex/amsmath/amstext.sty
(/usr/share/texlive/texmf-dist/tex/latex/amsmath/amsgen.sty))
(/usr/share/texlive/texmf-dist/tex/latex/amsmath/amsbsy.sty)
(/usr/share/texlive/texmf-dist/tex/latex/amsmath/amsopn.sty))
(/usr/share/texlive/texmf-dist/tex/latex/amscls/amsthm.sty)
(/usr/share/texlive/texmf-dist/tex/latex/base/inputenc.sty)
No file latex_00683f2d325b5e274d8b6f04699fec10646ec9c7_p.aux.
! You can't use `macro parameter character #' in horizontal mode.
l.10       * {{{#
                 !latex \gamma_{00
! Missing $ inserted.
<inserted text> 
                $
l.10       * {{{#!latex \gamma
                              _{00
(/usr/share/texlive/texmf-dist/tex/latex/amsfonts/umsa.fd)
(/usr/share/texlive/texmf-dist/tex/latex/amsfonts/umsb.fd)
! Missing $ inserted.
<inserted text> 
                $
l.11 \end{document}
                   
! Missing } inserted.
<inserted text> 
                }
l.11 \end{document}
                   
[1] (./latex_00683f2d325b5e274d8b6f04699fec10646ec9c7_p.aux) )
(\end occurred inside a group at level 3)

### simple group (level 3) entered at line 10 ({)
### simple group (level 2) entered at line 10 ({)
### simple group (level 1) entered at line 10 ({)
### bottom level
(see the transcript file for additional information)
Output written on latex_00683f2d325b5e274d8b6f04699fec10646ec9c7_p.dvi (1 page,
 308 bytes).
Transcript written on latex_00683f2d325b5e274d8b6f04699fec10646ec9c7_p.log.

} and #!latex \gamma_{10} the level-2 intercepts, represent the population average initial status and rate of change where #!latex \mathrm{X}=0

the level-2 slopes #!latex \gamma_{01} and #!latex \gamma_{11} represent the treatment effect #!latex \mathrm{X} on the intercept and the slope respectively
#!latex \xi_{0i} and #!latex \xi_{1i}, the level-2 residuals represent those portions of initial status or rate of change that are unexplained at level-2, they represent deviations of the individual change trajectories around their respective group average trends
#!latex \xi_{0i} and #!latex \xi_{1i} are assumed to be independently draw from a bivariate normal distribution with mean 0 and variances #!latex \sigma_0^2 and #!latex \sigma_1^2

Alternative Approach - Mixed Model

   1 > dl$variable <- factor(dl$variable)
   2 > require(nlme)
   3 > Lme.mod <- lme(value ~ group * variable, random = ~ 1 | Animal, data = dl)
   4 > anova(Lme.mod)
   5 numDF denDF  F-value p-value
   6 group              2    12    1.056  0.3782
   7 variable           5    60   52.550  <.0001

Alternative Approach - Mixed Model

   1 > require(lme4)
   2 > Lme.mod <- lmer(value ~ group * variable + (1 | Animal), data = dl)
   3 > anova(Lme.mod)
   4 Analysis of Variance Table
   5 Df Sum Sq Mean Sq F value
   6 group           2   1145   572.7  1.0555
   7 variable        5 142554 28510.9 52.5505
   8 > fixed.effects(Lme.mod)
   9 variable4        variable5        variable6        variable7

Alternative Approach - Mixed Model

extract fixed effects

   1 > fixed.effects(Lme.mod)
   2 variable4        variable5        variable6        variable7

Alternative Approach - Mixed Model

post hoc test

   1 > summary(glht(Lme.mod, linfct=mcp(group="Tukey")))
   2 Multiple Comparisons of Means: Tukey Contrasts
   3 Linear Hypotheses:
   4 Estimate Std. Error z value Pr(>|z|)
   5 1 - 0 == 0    28.00      27.69   1.011    0.570
   6 2 - 0 == 0    31.40      27.69   1.134    0.493
   7 2 - 1 == 0     3.40      27.69   0.123    0.992
   8 In mcp2matrix(model, linfct = linfct) :
   9 covariate interactions found -- default contrast might be inappropriate

Mixed Models

average the interaction term

   1 > ## consider interaction terms
   2 > summary(glht(Lme.mod, linfct=mcp(group="Tukey",interaction_average = TRUE)))
   3 Multiple Comparisons of Means: Tukey Contrasts
   4 Linear Hypotheses:
   5 Estimate Std. Error z value Pr(>|z|)
   6 1 - 0 == 0   33.133     24.202   1.369    0.357
   7 2 - 0 == 0   26.767     24.202   1.106    0.510
   8 2 - 1 == 0   -6.367     24.202  -0.263    0.963

Mixed Models

   1 > Lme.mod <- lmer(value ~ group + variable + (1 | Animal), data = dl)
   2 > anova(Lme.mod)
   3 Analysis of Variance Table
   4 Df Sum Sq Mean Sq F value
   5 group     2   1276   638.1  1.0555
   6 variable  5 142555 28510.9 47.1641
   7 > summary(glht(Lme.mod, linfct=mcp(group="Tukey")))
   8 Simultaneous Tests for General Linear Hypotheses
   9 Multiple Comparisons of Means: Tukey Contrasts
  10 Linear Hypotheses:
  11 Estimate Std. Error z value Pr(>|z|)
  12 1 - 0 == 0   33.133     24.202   1.369    0.357
  13 2 - 0 == 0   26.767     24.202   1.106    0.510
  14 2 - 1 == 0   -6.367     24.202  -0.263    0.963

Exercises

* try to set up an unconditional means model using lme or lmer from the respective package. * Extract the coefficients using coef() and interpret the results. * add time as fixed effect. * add time as random effect. Again: extract the coefficients, interpret. * add the group variable as factor, do an posthoc test

Solutions

* try to set up an unconditional means model using lme or lmer from the respective package.\scriptsize

   1 > mod.0 <- lmer(value ~ 1 + (1 | Animal ), data = dl)

* Extract the coefficients using coef() and interpret the results.\scriptsize

   1 > coef(mod.0)
   2 1     496.1230
   3 2     560.5914
   4 3     558.9076
   5 4     567.8080
   6 5     540.0241
   7 6     553.9762
   8 7     525.5909
   9 8     573.2205
  10 9     604.2520
  11 10    585.9699
  12 11    588.8565
  13 12    559.8698
  14 13    551.5707
  15 14    585.3685
  16 15    534.3711
  17 [1] "coef.mer"

* add time as fixed effect.\scriptsize

   1 > mod.1 <- lmer(value ~ variable + (1 | Animal ), data = dl)
   2 > coef(mod.1)
   3 1     394.8259 19.40286
   4 2     476.9201 19.40286
   5 3     474.7759 19.40286
   6 4     486.1098 19.40286
   7 5     450.7296 19.40286
   8 6     468.4963 19.40286
   9 7     432.3503 19.40286
  10 8     493.0020 19.40286
  11 9     532.5175 19.40286
  12 10    509.2371 19.40286
  13 11    512.9129 19.40286
  14 12    476.0012 19.40286
  15 13    465.4331 19.40286
  16 14    508.4713 19.40286
  17 15    443.5311 19.40286

* add time as random effect. Again: extract the coefficients, interpret.\scriptsize

   1 > mod.2 <- lmer(value ~ variable + (1 + variable | Animal ), data = dl)
   2 > coef(mod.2)
   3 1     452.6571  4.989677
   4 2     475.9532 19.079395
   5 3     474.2833 20.463988
   6 4     478.1603 21.318140
   7 5     468.0379 15.382203
   8 6     473.9412 17.008690
   9 7     462.0846 13.445867
  10 8     480.0258 22.650268
  11 9     491.3526 29.244908
  12 10    484.4619 25.718884
  13 11    485.6489 26.112158
  14 12    475.6310 19.023129
  15 13    472.0510 18.168807
  16 14    485.1363 24.115063
  17 15    465.8891 14.321680
  18 [1] "coef.mer"

* add the group variable as factor, do an posthoc test\scriptsize

   1 > mod.3 <- lmer(value ~ variable + group + (1 + variable | Animal ), data = dl)
   2 > coef(mod.3)
   3 1     448.2977  5.81501 10.60605 14.33476
   4 2     472.9694 19.59789 10.60605 14.33476
   5 3     465.2712 22.15993 10.60605 14.33476
   6 4     473.0687 22.24370 10.60605 14.33476
   7 5     461.8873 16.53096 10.60605 14.33476
   8 6     469.0268 15.91834 10.60605 14.33476
   9 7     447.5350 14.25275 10.60605 14.33476
  10 8     470.6132 22.42630 10.60605 14.33476
  11 9     483.2428 28.74823 10.60605 14.33476
  12 10    474.3565 25.62254 10.60605 14.33476
  13 11    475.0372 25.41345 10.60605 14.33476
  14 12    466.9784 17.95933 10.60605 14.33476
  15 13    459.9408 17.78472 10.60605 14.33476
  16 14    478.6720 22.60904 10.60605 14.33476
  17 15    453.7132 13.96066 10.60605 14.33476
  18 [1] "coef.mer"
  19 > summary(glht(mod.3, linfct=mcp(group="Tukey")))
  20 Multiple Comparisons of Means: Tukey Contrasts
  21 data = dl)
  22 Linear Hypotheses:
  23 Estimate Std. Error z value Pr(>|z|)
  24 1 - 0 == 0   10.606     16.669   0.636    0.800
  25 2 - 0 == 0   14.335     16.669   0.860    0.666
  26 2 - 1 == 0    3.729     16.669   0.224    0.973

\multicolumn{5}{c}{Factor A (Repeated Measures)} \\ \hline
\|Subjects \|A_1 \|A_2 \|\cdots \|A_p \|
\|S_{1} \|( y_{11} \|y_{12} \|\cdots \|y_{1p} ) \|= \mathbf{y^t_{1}}
\|S_{2} \|( y_{21} \|y_{22} \|\cdots \|y_{2p} ) \|= \mathbf{y^t_{2}}
\|S_{3} \|( y_{31} \|y_{32} \|\cdots \|y_{3p} ) \|= \mathbf{y^t_{3}}
\|\vdots \|\vdots \|\vdots \| \| \vdots o\| \vdots
\|S_{n} \|( y_{n1} \|y_{n2} \|\cdots \|y_{np} ) \|= \mathbf{y^t_{n}}

\multicolumn{5}{c}{Factor A (Repeated Measures)} \\ \hline
Factor B \|Subjects \|A_1 \|A_2 \|\cdots \|A_p \|
B_1 \|S_{11} \|( y_{111} \|y_{112} \|\cdots \|y_{11p} ) \|= \mathbf{y^t_{11}}
\|S_{12} \|( y_{121} \|y_{122} \|\cdots \|y_{12p} ) \|= \mathbf{y^t_{12}}
\|S_{13} \|( y_{131} \|y_{132} \|\cdots \|y_{13p} ) \|= \mathbf{y^t_{13}}
\|\vdots \|\vdots \|\vdots \| \| \vdots \| \vdots
\|S_{1n} \|( y_{2n1} \|y_{2n2} \|\cdots \|y_{2np} ) \|= \mathbf{y^t_{2n}}
B_2 \|S_{21} \|( y_{211} \|y_{212} \|\cdots \|y_{21p} ) \|= \mathbf{y^t_{21}}
\|S_{22} \|( y_{221} \|y_{222} \|\cdots \|y_{22p} ) \|= \mathbf{y^t_{22}}
\|S_{23} \|( y_{231} \|y_{232} \|\cdots \|y_{23p} ) \|= \mathbf{y^t_{23}}
\|\vdots \|\vdots \|\vdots \| \| \vdots o\| \vdots
\|S_{2n} \|( y_{2n1} \|y_{2n2} \|\cdots \|y_{2np} ) \|= \mathbf{y^t_{2n}}
B_k \|S_{k1} \|( y_{k11} \|y_{k12} \|\cdots \|y_{k1p} ) \|= \mathbf{y^t_{k1}}
\|S_{k2} \|( y_{k21} \|y_{k22} \|\cdots \|y_{k2p} ) \|= \mathbf{y^t_{k2}}
\|S_{k3} \|( y_{k31} \|y_{k32} \|\cdots \|y_{k3p} ) \|= \mathbf{y^t_{k3}}
\|\vdots \|\vdots \|\vdots \| \| \vdots \| \vdots
\|S_{kn} \|( y_{kn1} \|y_{kn2} \|\cdots \|y_{knp} ) \|= \mathbf{y^t_{kn}}

Quick Links

Search Wiki

Page Tools

Repeated Measures ANOVA (rma)

Statistical Model

Statistical Model

Repeated Measures ANOVA (rma)

Repeated Measures ANOVA (rma)

Example

Example

Example

MANOVA

MANOVA

MANOVA

Example Data

Example Data

Example Data

Example Data

Basic multivariate model

Basic multivariate model

Basic multivariate model

Testing within-S effects

Test Statistics

The 4 Test Statistics

The 4 Test Statistics

The 4 Test Statistics

The 4 Test Statistics

The 4 Test Statistics

Add between-S effects

Add between-S effects

Add between-S effects

MANOVA Tests

Assumptions MANOVA

Alternative Approach - Mixed Model

Alternative Approach - Mixed Model

Alternative Approach - Mixed Model

Alternative Approach - Mixed Model

Alternative Approach - Mixed Model

Alternative Approach - Mixed Model

Mixed Models

Mixed Models

Exercises

Solutions