|
Größe: 17743
Kommentar:
|
Größe: 18133
Kommentar:
|
| Gelöschter Text ist auf diese Art markiert. | Hinzugefügter Text ist auf diese Art markiert. |
| Zeile 3: | Zeile 3: |
| * load the data (file: session4data.rdata) * make a new summary data frame (per subject and time) containing: * the number of trials * the number correct trials (absolute and relative) * the mean TTime and the standard deviation of TTime * the respective standard error of the mean * keep the information about Sex and Age\_PRETEST * make a plot with time on the x-axis and TTime on the y-axis showing the means and the 95\% confidence intervals (geom\_pointrange()) * add the number of trials and the percentage of correct ones using geom\_text() |
* load the data (file: session4data.rdata) * make a new summary data frame (per subject and time) containing: * the number of trials * the number correct trials (absolute and relative) * the mean TTime and the standard deviation of TTime * the respective standard error of the mean * keep the information about Sex and Age_PRETEST * make a plot with time on the x-axis and TTime on the y-axis showing the means and the 95\% confidence intervals (geom_pointrange()) * add the number of trials and the percentage of correct ones using geom_text() |
| Zeile 13: | Zeile 13: |
| * \item load the data (file: session4data.rdata) | * load the data (file: session4data.rdata) |
| Zeile 34: | Zeile 34: |
| * ]<9-> 1 sample * ]<9-> 2 samples * ]<9-> {{{#!latex k}}} samples |
|
| Zeile 38: | Zeile 35: |
| ||| \multicolumn{1}{c}{}|\multicolumn{2}{c}{'''Situation}''' || ||| \multicolumn{1}{c}{}|\multicolumn{1}{c}{H_0 is true} |\multicolumn{1}{c}{H_0 is false} || ||'''Conclusion''' |H_0 is not rejected | Correct decision |Type II error || |||H_0 is rejected |Type I error | Correct decision || |
|||| ||Situation |||| |||| ||H_0 is true ||H_0 is false || ||<rowspan=2>Conclusion||H_0 is not rejected || Correct decision ||Type II error || ||H_0 is rejected ||Type I error || Correct decision || |
| Zeile 43: | Zeile 41: |
| ||n |number of observations (sample size)\onslide<2->|| ||K |number of samples (each having n elements) \onslide<3->|| ||s |standard deviation (sample)\onslide<4->|| ||r |sample correlation coefficient \onslide<5->|| ||Z |standard normal deviate || |
||n ||number of observations (sample size)|| ||K ||number of samples (each having n elements)|| ||alpha ||level of significance || ||nu ||degrees of freedom|| ||mu ||population mean|| ||xbar ||sample mean|| ||sigma ||standard deviation (population)|| ||s ||standard deviation (sample)|| ||rho ||population correlation coefficient|| ||r ||sample correlation coefficient|| ||Z ||standard normal deviate || |
| Zeile 49: | Zeile 55: |
| <img alt='sesssion2/twosided.pdf}' src='-1' /> <img alt='sesssion2/greater.pdf}' src='-1' /> <img alt='sesssion2/less.pdf}' src='-1' /> == Alternatives == The p-value is the probability of the sample estimate (of the respective estimator) under the null. |
[[attachment:twosided.pdf|{{attachment:twosided.pdf||width=800,height=400}}]] [[attachment:greater.pdf|{{attachment:greater.pdf||width=800,height=400}}]] [[attachment:less.pdf|{{attachment:less.pdf||width=800,height=400}}]] The p-value is the probability of the sample estimate (of the respective estimator) under the null. The p-value is NOT the probability that the null is true. |
| Zeile 56: | Zeile 65: |
| To investigate the significance of the difference between an assumed population mean {{{#!latex \mu_0}}} and a sample mean {{{#!latex \bar{x}}}}. * It is necessary that the population variance {{{#!latex \sigma^2}}} is known. * The test is accurate if the population is normally distributed. If the population is not normal, the test will still give an approximate guide. == Z-test for a population mean == * Write a function which takes a vector, the population standard deviation and the population mean as arguments and which gives the Z score as result. |
To investigate the significance of the difference between an assumed population mean {{{#!latex $\mu_0$}}} and a sample mean {{{#!latex $\bar{x}$ }}} * It is necessary that the population variance {{{#!latex $\sigma^2$ }}} is known. * The test is accurate if the population is normally distributed. If the population is not normal, the test will still give an approximate guide. == Excercise == * Write a function which takes a vector, the population standard deviation and the population mean as arguments and which gives the Z score as result. |
| Zeile 63: | Zeile 80: |
| * add a line to your function that allows you to process numeric vectors containing missing values! * the function pnorm(Z) gives the probability of {{{#!latex x \leq Z {{{#!latex . Change your function so that it has the p-value (for a two sided test) as result. * now let the result be a named vector containing the estimated difference, Z, p and the n. |
* add a line to your function that allows you to process numeric vectors containing missing values! * the function pnorm(Z) gives the probability of {{{#!latex $$x \leq Z$$ }}} . Change your function so that it has the p-value (for a two sided test) as result. * now let the result be a named vector containing the estimated difference, Z, p and the n. |
| Zeile 67: | Zeile 86: |
| == Z-test for a population mean == | === Z-test for a population mean - solution === |
| Zeile 77: | Zeile 96: |
| == Z-test for a population mean == | |
| Zeile 86: | Zeile 105: |
| == Z-test for a population mean == The function pnorm(Z) gives the probability of {{{#!latex x \leq Z {{{#!latex . Change your function so that it has the p-value (for a two sided test) as result. |
The function pnorm(Z) gives the probability of {{{#!latex $$x \leq Z$$ }}} . Change your function so that it has the p-value (for a two sided test) as result. |
| Zeile 99: | Zeile 120: |
| == Z-test for a population mean == | |
| Zeile 113: | Zeile 134: |
| == Z-test for a population mean == * Z-test for two population means (variances known and equal) * Z-test for two population means (variances known and unequal) To investigate the statistical significance of the difference between an assumed population mean {{{#!latex \mu_0}}} and a sample mean {{{#!latex \bar{x}}}}. There is a function z.test() in the BSDA package. * It is necessary that the population variance {{{#!latex \sigma^2}}} is known. * The test is accurate if the population is normally distributed. If the population is not normal, the test will still give an approximate guide. |
=== Requirements === * Z-test for two population means (variances known and equal) * Z-test for two population means (variances known and unequal) To investigate the statistical significance of the difference between an assumed population mean {{{#!latex $\mu_0$}}} and a sample mean {{{#!latex $\bar{x}$}}}. There is a function z.test() in the BSDA package * It is necessary that the population variance {{{#!latex $\sigma^2$}}} is known. * The test is accurate if the population is normally distributed. If the population is not normal, the test will still give an approximate guide. |
| Zeile 120: | Zeile 149: |
| * Now sample 100 values from a Normal distribution with mean 10 and standard deviation 2 and use a z-test to compare it against the population mean 10. What is the p-value? * Now do the sampling and the testing 1000 times, what would be the number of statistically significant results? Use replicate() (which is a wrapper of tapply()) or a for() loop! Record at least the p-values and the estimated differences! Use table() to count the p-vals below 0.05. What type of error do you associate with it? What is the smallest absolute difference with a p-value below 0.05? * Repeat the simulation above, change the sample size to 1000 in each of the 1000 samples! How many p-values below 0.05? What is now the smallest absolute difference with a p-value below 0.05? == Simulation Exercises -- Solutions == * Now sample 100 values from a Normal distribution with mean 10 and standard deviation 2 and use a z-test to compare it against the population mean 10. What is the p-value? What the estimated difference? |
* Now sample 100 values from a Normal distribution with mean 10 and standard deviation 2 and use a z-test to compare it against the population mean 10. What is the p-value? * Now do the sampling and the testing 1000 times, what would be the number of statistically significant results? Use replicate() (which is a wrapper of tapply()) or a for() loop! Record at least the p-values and the estimated differences! Use table() to count the p-vals below 0.05. What type of error do you associate with it? What is the smallest absolute difference with a p-value below 0.05? * Repeat the simulation above, change the sample size to 1000 in each of the 1000 samples! How many p-values below 0.05? What is now the smallest absolute difference with a p-value below 0.05? === Simulation Exercises -- Solutions === * Now sample 100 values from a Normal distribution with mean 10 and standard deviation 2 and use a z-test to compare it against the population mean 10. What is the p-value? What the estimated difference? |
| Zeile 133: | Zeile 162: |
| == Simulation Exercises -- Solutions == | |
| Zeile 135: | Zeile 164: |
| using replicate()\footnotesize | using replicate() |
| Zeile 148: | Zeile 177: |
| == Simulation Exercises -- Solutions == | |
| Zeile 150: | Zeile 179: |
| using replicate() II\footnotesize | using replicate() II |
| Zeile 159: | Zeile 188: |
| == Simulation Exercises -- Solutions == | |
| Zeile 161: | Zeile 190: |
| using for() \scriptsize | using for() |
| Zeile 177: | Zeile 206: |
| == Simulation Exercises -- Solutions == | |
| Zeile 187: | Zeile 216: |
| == Simulation Exercises -- Solutions == | |
| Zeile 202: | Zeile 231: |
| == Simulation Exercises -- Solutions == | |
| Zeile 211: | Zeile 240: |
| * Concatenate the both resulting data frames from above using rbind() * Plot the distributions of the pvals and the difference per sample size. Use ggplot2 with an appropriate geom (density/histogram) * What is the message? == Simulation Exercises -- Solutions == |
* Concatenate the both resulting data frames from above using rbind() * Plot the distributions of the pvals and the difference per sample size. Use ggplot2 with an appropriate geom (density/histogram) * What is the message? === Simulation Exercises -- Solutions === |
| Zeile 225: | Zeile 254: |
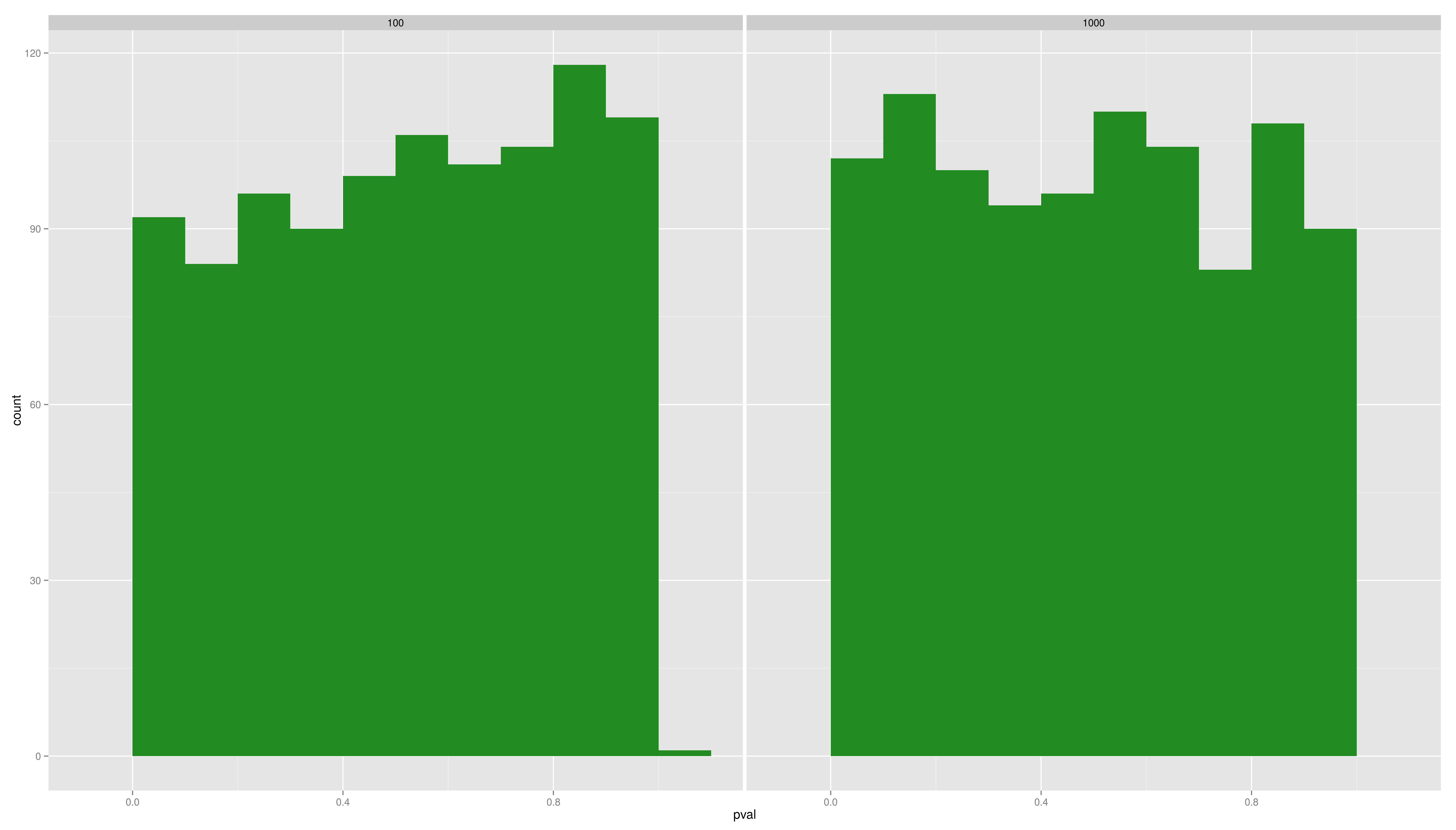
| == Simulation Exercises -- Solutions == <img alt='sesssion2/hist.png' src='-1' /> == Simulation Exercises -- Solutions == |
[[attachment:hist.png|{{attachment:hist.png||width=800}}]] |
| Zeile 235: | Zeile 264: |
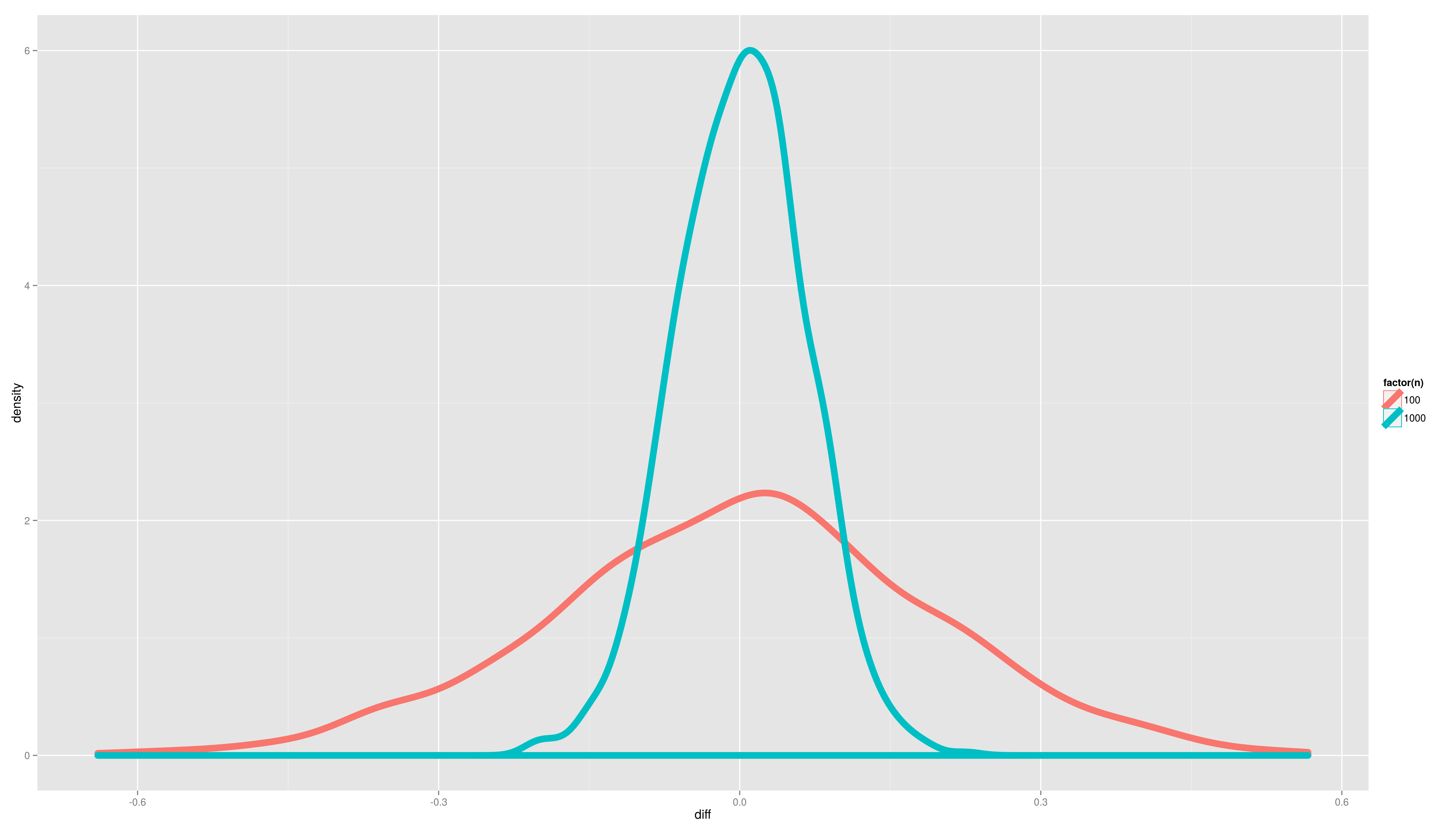
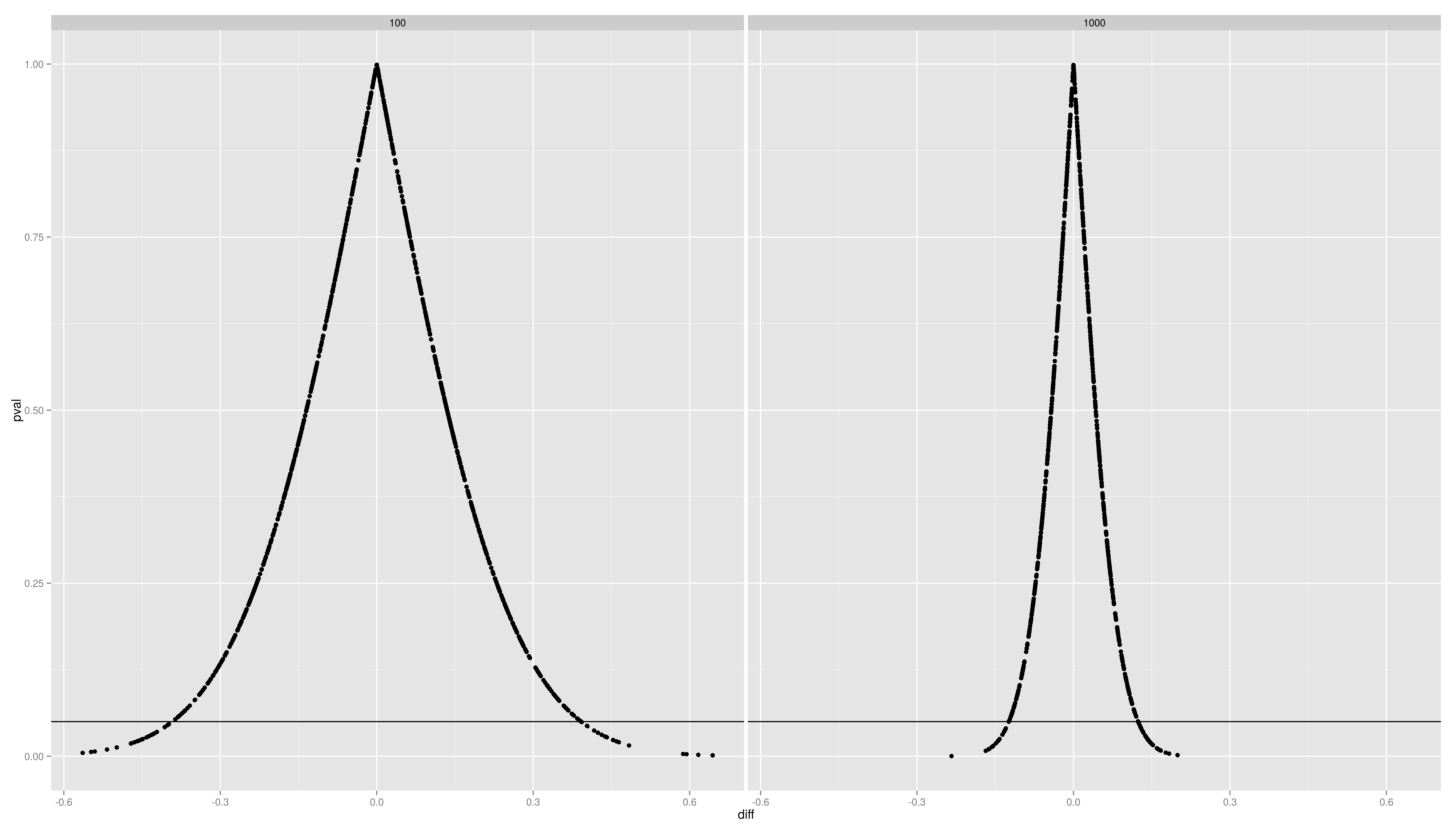
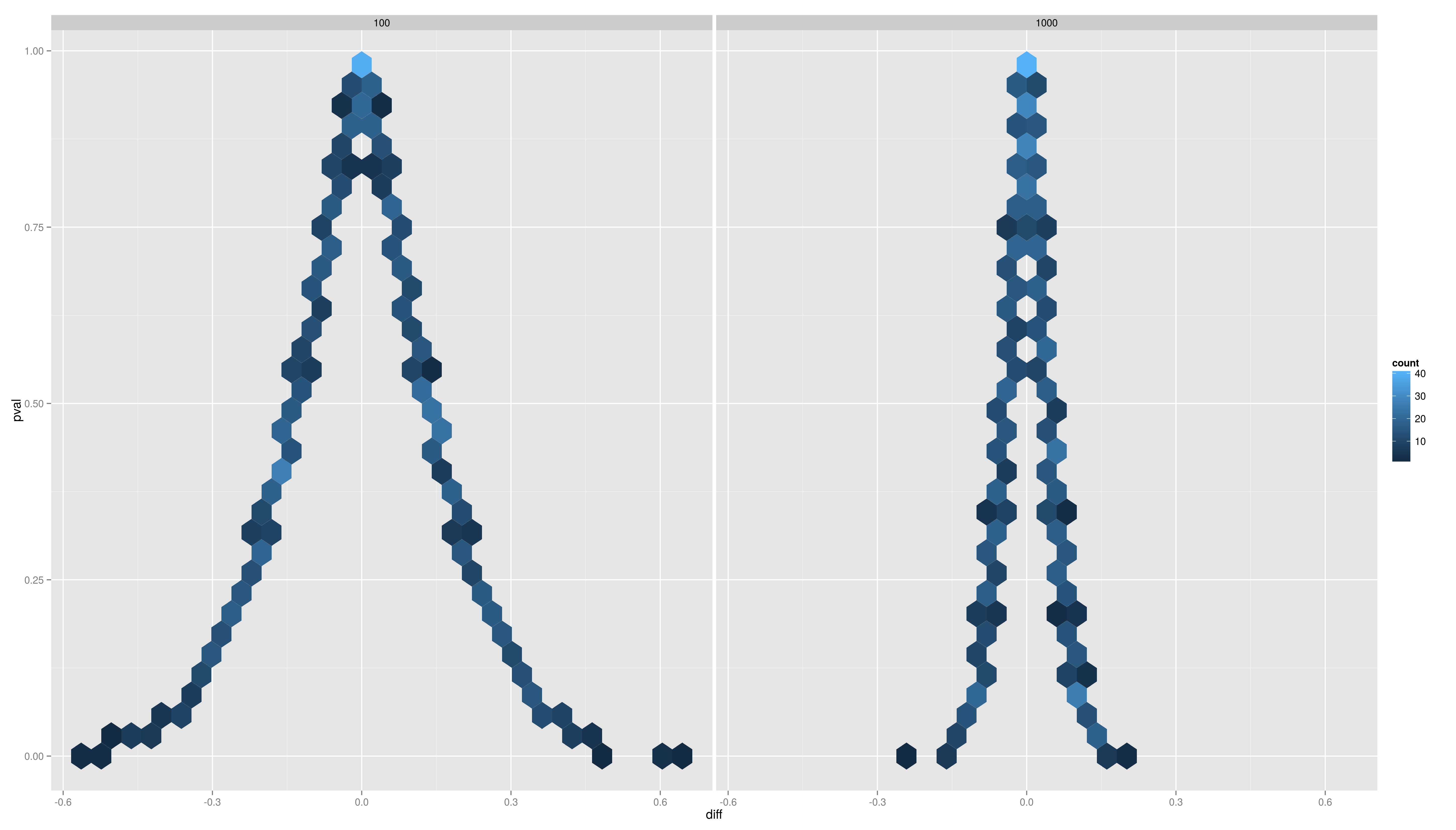
| <img alt='sesssion2/dens.png' src='-1' /> == Simulation Exercises -- Solutions == <img alt='sesssion2/point.png' src='-1' /> == Simulation Exercises -- Solutions == <img alt='sesssion2/dens2d.png' src='-1' /> |
[[attachment:dens.png|{{attachment:dens.png||width=800}}]] [[attachment:point.png|{{attachment:point.png||width=800}}]] [[attachment:dens2d.png|{{attachment:dens2d.png||width=800}}]] |
| Zeile 259: | Zeile 291: |
| A t-test is any statistical hypothesis test in which the test statistic follows a \emph{Student's t distribution} if the null hypothesis is supported. * \emph{one sample t-test}: test a sample mean against a population mean == One Sample t-test == |
A t-test is any statistical hypothesis test in which the test statistic follows a Student's t distribution if the null hypothesis is supported. * one sample t-test: test a sample mean against a population mean {{{#!latex $$t = \frac{\bar{x}-\mu_0}{s/\sqrt{n}}$$ }}} where {{{#!latex $\bar{x}$ }}} is the sample mean, s is the sample standard deviation and n is the sample size. The degrees of freedom used in this test is n-1 {{{#!highlight r > set.seed(1) > x <- rnorm(12) > t.test(x,mu=0) ## population mean 0 One Sample t-test data: x t = 1.1478, df = 11, p-value = 0.2754 alternative hypothesis: true mean is not equal to 0 95 percent confidence interval: -0.2464740 0.7837494 sample estimates: mean of x 0.2686377 > t.test(x,mu=1) ## population mean 1 One Sample t-test data: x t = -3.125, df = 11, p-value = 0.009664 alternative hypothesis: true mean is not equal to 1 95 percent confidence interval: -0.2464740 0.7837494 sample estimates: mean of x 0.2686377 }}} |
| Zeile 265: | Zeile 335: |
| * given one vector x containing all the measurement values and one vector g containing the group membership {{{#!latex t.test(x \sim g)}}} (read: x dependend on g) == Two Sample t-tests: two vector syntax == |
* given one vector x containing all the measurement values and one vector g containing the group membership {{{#!latex t.test(x $\sim$ g) }}} (read: x dependend on g) === Two Sample t-tests: two vector syntax === |
| Zeile 279: | Zeile 353: |
| == Two Sample t-tests: formula syntax == | === Two Sample t-tests: formula syntax === |
| Zeile 288: | Zeile 362: |
| == Welch/Satterthwaite vs. Student == | === Welch/Satterthwaite vs. Student === |
| Zeile 300: | Zeile 374: |
| == t-test == | === Requirements === |
| Zeile 302: | Zeile 376: |
| * it is also recommended for group sizes {{{#!latex \geq 30}}} (robust against deviation from normality) | * it is also recommended for group sizes > 30 (robust against deviation from normality) |
| Zeile 304: | Zeile 378: |
| * use a t-test to compare TTime according to Stim.Type, visualize it. What is the problem? * now do the same for Subject 1 on pre and post test (use filter() or indexing to get the resp. subsets) * use the following code to do the test on every subset Subject and testid, try to figure what is happening in each step:\tiny |
* use a t-test to compare TTime according to Stim.Type, visualize it. What is the problem? * now do the same for Subject 1 on pre and post test (use filter() or indexing to get the resp. subsets) * use the following code to do the test on every subset Subject and testid, try to figure what is happening in each step:\tiny |
| Zeile 316: | Zeile 391: |
| * make plots to visualize the results. * how many tests have a statistically significant result? How many did you expect? Is there a tendency? What could be the next step? == Exercises - Solutions == |
* make plots to visualize the results. * how many tests have a statistically significant result? How many did you expect? Is there a tendency? What could be the next step? === Solutions === |
| Zeile 330: | Zeile 405: |
| == Exercises - Solutions == | |
| Zeile 348: | Zeile 422: |
| == Exercises - Solutions == | |
| Zeile 358: | Zeile 431: |
| == Exercises - Solutions == |
Classical Tests
Exercises
- load the data (file: session4data.rdata)
- make a new summary data frame (per subject and time) containing:
- the number of trials
- the number correct trials (absolute and relative)
- the mean TTime and the standard deviation of TTime
- the respective standard error of the mean
- keep the information about Sex and Age_PRETEST
- make a plot with time on the x-axis and TTime on the y-axis showing the means and the 95\% confidence intervals (geom_pointrange())
- add the number of trials and the percentage of correct ones using geom_text()
Exercises - Solutions
- load the data (file: session4data.rdata)
- make a new summary data frame (per subject and time) containing:
1 > sumdf <- data %>%
2 + group_by(Subject,Sex,Age_PRETEST,testid) %>%
3 + summarise(count=n(),
4 + n.corr = sum(Stim.Type=="hit"),
5 + perc.corr = n.corr/count,
6 + mean.ttime = mean(TTime),
7 + sd.ttime = sd(TTime),
8 + se.ttime = sd.ttime/sqrt(count))
9 > head(sumdf)
10 Subject Sex Age_PRETEST testid count n.corr perc.corr mean.ttime
11 1 1 f 3.11 test1 95 63 0.6631579 8621.674
12 2 1 f 3.11 1 60 32 0.5333333 9256.367
13 3 1 f 3.11 2 59 32 0.5423729 9704.712
14 4 1 f 3.11 3 60 38 0.6333333 14189.550
15 5 1 f 3.11 4 59 31 0.5254237 13049.831
16 6 1 f 3.11 5 59 33 0.5593220 14673.525
17 Variables not shown: sd.ttime se.ttime (dbl)
four possible situations
|
Situation |
||
|
H_0 is true |
H_0 is false |
|
Conclusion |
H_0 is not rejected |
Correct decision |
Type II error |
H_0 is rejected |
Type I error |
Correct decision |
|
Common symbols
n |
number of observations (sample size) |
K |
number of samples (each having n elements) |
alpha |
level of significance |
nu |
degrees of freedom |
mu |
population mean |
xbar |
sample mean |
sigma |
standard deviation (population) |
s |
standard deviation (sample) |
rho |
population correlation coefficient |
r |
sample correlation coefficient |
Z |
standard normal deviate |
Alternatives
The p-value is the probability of the sample estimate (of the respective estimator) under the null. The p-value is NOT the probability that the null is true.
Z-test for a population mean
The z-test is a something like a t-test (it is like you would know almost everything about the perfect conditions. It uses the normal distribution as test statistic and is therefore a good example. To investigate the significance of the difference between an assumed population mean
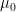
and a sample mean
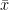
- It is necessary that the population variance
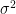
is known.
- The test is accurate if the population is normally distributed. If the population is not normal, the test will still give an approximate guide.
Excercise
- Write a function which takes a vector, the population standard deviation and the population mean as arguments and which gives the Z score as result.
- name the function ztest or my.z.test - not z.test because z.test is already used
- set a default value for the population mean
- add a line to your function that allows you to process numeric vectors containing missing values!
- the function pnorm(Z) gives the probability of
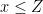
. Change your function so that it has the p-value (for a two sided test) as result.
- now let the result be a named vector containing the estimated difference, Z, p and the n.
You can always test your function using simulated values: rnorm(100,mean=0) gives you a vector containing 100 normal distributed values with mean 0.
Z-test for a population mean - solution
Write a function which takes a vector, the population standard deviation and the population mean as arguments and which gives the Z score as result.
Add a line to your function that allows you to also process numeric vectors containing missing values!
The function pnorm(Z) gives the probability of
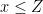
. Change your function so that it has the p-value (for a two sided test) as result.
Now let the result be a named vector containing the estimated difference, Z, p and the n.
1 > ztest <- function(x,x.sd,mu=0){
2 + x <- x[!is.na(x)]
3 + if(length(x) < 3) stop("too few values in x")
4 + est.diff <- mean(x)-mu
5 + z <- sqrt(length(x)) * (est.diff)/x.sd
6 + round(c(diff=est.diff,Z=z,pval=2*pnorm(-abs(z)),n=length(x)),4)
7 + }
8 > set.seed(1)
9 > ztest(rnorm(100),x.sd = 1)
10 diff Z pval n
Requirements
- Z-test for two population means (variances known and equal)
- Z-test for two population means (variances known and unequal)
To investigate the statistical significance of the difference between an assumed population mean
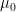
and a sample mean
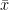
. There is a function z.test() in the BSDA package
- It is necessary that the population variance
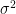
is known.
- The test is accurate if the population is normally distributed. If the population is not normal, the test will still give an approximate guide.
Simulation Exercises
- Now sample 100 values from a Normal distribution with mean 10 and standard deviation 2 and use a z-test to compare it against the population mean 10. What is the p-value?
- Now do the sampling and the testing 1000 times, what would be the number of statistically significant results? Use replicate() (which is a wrapper of tapply()) or a for() loop! Record at least the p-values and the estimated differences! Use table() to count the p-vals below 0.05. What type of error do you associate with it? What is the smallest absolute difference with a p-value below 0.05?
- Repeat the simulation above, change the sample size to 1000 in each of the 1000 samples! How many p-values below 0.05? What is now the smallest absolute difference with a p-value below 0.05?
Simulation Exercises -- Solutions
- Now sample 100 values from a Normal distribution with mean 10 and standard deviation 2 and use a z-test to compare it against the population mean 10. What is the p-value? What the estimated difference?
- Now do the sampling and the testing 1000 times, what would be the number of statistically significant results? Use replicate() (which is a wrapper of tapply()) or a for() loop. Record at least the p-values and the estimated differences! Transform the result into a data frame.
using replicate()
1 > res <- replicate(1000, ztest(rnorm(100,mean=10,sd=2),x.sd=2,mu=10))
2 > res <- as.data.frame(t(res))
3 > head(res)
4 diff Z pval n
5 1 -0.2834 -1.4170 0.1565 100
6 2 0.2540 1.2698 0.2042 100
7 3 -0.1915 -0.9576 0.3383 100
8 4 0.1462 0.7312 0.4646 100
9 5 0.1122 0.5612 0.5747 100
10 6 -0.0141 -0.0706 0.9437 100
- Now do the sampling and the testing 1000 times, what would be the number of statistically significant results? Use replicate() (which is a wrapper of tapply()) or a for() loop. Record at least the p-values and the estimated differences! Transform the result into a data frame.
using replicate() II
- Now do the sampling and the testing 1000 times, what would be the number of statistically significant results? Use replicate() (which is a wrapper of tapply()) or a for() loop. Record at least the p-values and the estimated differences! Transform the result into a data frame.
using for()
1 > res <- matrix(numeric(2000),ncol=2)
2 > for(i in seq.int(1000)){
3 + res[i,] <- ztest(rnorm(100,mean=10,sd=2),x.sd=2,mu=10)[c("pval","diff")] }
4 > res <- as.data.frame(res)
5 > names(res) <- c("pval","diff")
6 > head(res)
7 pval diff
8 1 0.0591 -0.3775
9 2 0.2466 0.2317
10 3 0.6368 0.0944
11 4 0.5538 -0.1184
12 5 0.9897 -0.0026
13 6 0.7748 0.0572
- Use table() to count the p-vals below 0.05. What type of error do you associate with it? What is the smallest absolute difference with a p-value below 0.05?
- Repeat the simulation above, change the sample size to 1000 in each of the 1000 samples! How many p-values below 0.05? What is now the smallest absolute difference with a p-value below 0.05?
1 > res2 <- replicate(1000, ztest(rnorm(1000,mean=10,sd=2),
2 + x.sd=2,mu=10))
3 > res2 <- as.data.frame(t(res2))
4 > head(res2)
5 diff Z pval n
6 1 -0.0731 -1.1559 0.2477 1000
7 2 0.0018 0.0292 0.9767 1000
8 3 0.0072 0.1144 0.9089 1000
9 4 -0.1145 -1.8100 0.0703 1000
10 5 -0.1719 -2.7183 0.0066 1000
11 6 0.0880 1.3916 0.1640 1000
- Repeat the simulation above, change the sample size to 1000 in each of the 1000 samples! How many p-values below 0.05? What is now the smallest absolute difference with a p-value below 0.05?
Simulation Exercises Part II
- Concatenate the both resulting data frames from above using rbind()
- Plot the distributions of the pvals and the difference per sample size. Use ggplot2 with an appropriate geom (density/histogram)
- What is the message?
Simulation Exercises -- Solutions
- Concatenate the both resulting data frames from above using rbind()
- Plot the distributions of the pvals and the difference per sample size. Use ggplot2 with an appropriate geom (density/histogram)
- Plot the distributions of the pvals and the difference per sample size. Use ggplot2 with an appropriate geom (density/histogram)
Simulation Exercises -- Solutions
t-tests
A t-test is any statistical hypothesis test in which the test statistic follows a Student's t distribution if the null hypothesis is supported.
- one sample t-test: test a sample mean against a population mean

where
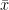
is the sample mean, s is the sample standard deviation and n is the sample size. The degrees of freedom used in this test is n-1
1 > set.seed(1)
2 > x <- rnorm(12)
3 > t.test(x,mu=0) ## population mean 0
4
5 One Sample t-test
6
7 data: x
8 t = 1.1478, df = 11, p-value = 0.2754
9 alternative hypothesis: true mean is not equal to 0
10 95 percent confidence interval:
11 -0.2464740 0.7837494
12 sample estimates:
13 mean of x
14 0.2686377
15
16 > t.test(x,mu=1) ## population mean 1
17
18 One Sample t-test
19
20 data: x
21 t = -3.125, df = 11, p-value = 0.009664
22 alternative hypothesis: true mean is not equal to 1
23 95 percent confidence interval:
24 -0.2464740 0.7837494
25 sample estimates:
26 mean of x
27 0.2686377
Two Sample t-tests
There are two ways to perform a two sample t-test in R:
- given two vectors x and y containing the measurement values from the respective groups t.test(x,y)
- given one vector x containing all the measurement values and one vector g containing the group membership
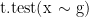
(read: x dependend on g)
Two Sample t-tests: two vector syntax
1 > set.seed(1)
2 > x <- rnorm(12)
3 > y <- rnorm(12)
4 > g <- sample(c("A","B"),12,replace = T)
5 > t.test(x,y)
6 t = 0.5939, df = 20.012, p-value = 0.5592
7 alternative hypothesis: true difference in means is not equal to 0
8 95 percent confidence interval:
9 sample estimates:
10 mean of x mean of y
Two Sample t-tests: formula syntax
Welch/Satterthwaite vs. Student
- if not stated otherwise t.test() will not assume that the variances in the both groups are equal
- if one knows that both populations have the same variance set the var.equal argument to TRUE to perform a student's t-test
Student's t-test
Requirements
- the t-test, especially the Welch test is appropriate whenever the values are normally distributed
it is also recommended for group sizes > 30 (robust against deviation from normality)
Exercises
- use a t-test to compare TTime according to Stim.Type, visualize it. What is the problem?
- now do the same for Subject 1 on pre and post test (use filter() or indexing to get the resp. subsets)
- use the following code to do the test on every subset Subject and testid, try to figure what is happening in each step:\tiny
- make plots to visualize the results.
- how many tests have a statistically significant result? How many did you expect? Is there a tendency? What could be the next step?
Solutions
- use a t-test to compare TTime according to Stim.Type, visualize it. What is the problem?
1 > t.test(data$TTime ~ data$Stim.Type)
2 t = -6.3567, df = 9541.891, p-value = 2.156e-10
3 alternative hypothesis: true difference in means is not equal to 0
4 95 percent confidence interval:
5 sample estimates:
6 mean in group hit mean in group incorrect
7 > ggplot(data,aes(x=Stim.Type,y=TTime)) +
8 + geom_boxplot()
- now do the same for Subject 1 on pre and post test (use filter() or indexing to get the resp. subsets)
1 > t.test(data$TTime[data$Subject==1 & data$testid=="test1"] ~
2 + data$Stim.Type[data$Subject==1 & data$testid=="test1"])
3 t = -0.5846, df = 44.183, p-value = 0.5618
4 alternative hypothesis: true difference in means is not equal to 0
5 95 percent confidence interval:
6 sample estimates:
7 mean in group hit mean in group incorrect
8 > t.test(data$TTime[data$Subject==1 & data$testid=="test2"] ~
9 + data$Stim.Type[data$Subject==1 & data$testid=="test2"])
10 t = -1.7694, df = 47.022, p-value = 0.08332
11 alternative hypothesis: true difference in means is not equal to 0
12 95 percent confidence interval:
13 sample estimates:
14 mean in group hit mean in group incorrect
- make plots to visualize the results
- how many tests have an statistically significant result? How many did you expect?
Exercises - Solutions
- What could be the next step?