|
Größe: 17797
Kommentar:
|
← Revision 12 vom 2015-05-03 06:24:36 ⇥
Größe: 19682
Kommentar:
|
| Gelöschter Text ist auf diese Art markiert. | Hinzugefügter Text ist auf diese Art markiert. |
| Zeile 9: | Zeile 9: |
| * keep the information about Sex and Age\_PRETEST * make a plot with time on the x-axis and TTime on the y-axis showing the means and the 95\% confidence intervals (geom\_pointrange()) * add the number of trials and the percentage of correct ones using geom\_text() |
* keep the information about Sex and Age_PRETEST * make a plot with time on the x-axis and TTime on the y-axis showing the means and the 95\% confidence intervals (geom_pointrange()) * add the number of trials and the percentage of correct ones using geom_text() |
| Zeile 61: | Zeile 61: |
| == Alternatives == The p-value is the probability of the sample estimate (of the respective estimator) under the null. |
The p-value is the probability of the sample estimate (of the respective estimator) under the null. The p-value is NOT the probability that the null is true. |
| Zeile 64: | Zeile 64: |
| The z-test is a something like a t-test (it is like you would know almost everything about the perfect conditions. It uses the normal distribution as test statistic and is therefore a good example. To investigate the significance of the difference between an assumed population mean {{{#!latex \mu_0}}} and a sample mean {{{#!latex \bar{x}}}}. * It is necessary that the population variance {{{#!latex \sigma^2}}} is known. * The test is accurate if the population is normally distributed. If the population is not normal, the test will still give an approximate guide. == Z-test for a population mean == * Write a function which takes a vector, the population standard deviation and the population mean as arguments and which gives the Z score as result. |
The z-test is a something like a t-test (it is like you would know almost everything about the perfect conditions. It uses the normal distribution as distribution of the test statistic and is therefore a good example. * To investigate the significance of the difference between an assumed population mean {{{#!latex $\mu_0$}}} and a sample mean {{{#!latex $\bar{x}$ }}} It is necessary that the population variance {{{#!latex $\sigma^2$ }}} is known. * The test is accurate if the population values are normally distributed. If the population values are not normal, the test will still give an approximate guide. == Excercise == * Write a function which takes a vector, the population standard deviation and the population mean as arguments and which gives the Z score as result. |
| Zeile 72: | Zeile 80: |
| * add a line to your function that allows you to process numeric vectors containing missing values! * the function pnorm(Z) gives the probability of {{{#!latex x \leq Z {{{#!latex . Change your function so that it has the p-value (for a two sided test) as result. * now let the result be a named vector containing the estimated difference, Z, p and the n. |
* add a line to your function that allows you to process numeric vectors containing missing values! * the function pnorm(Z) gives the probability of {{{#!latex $$x \leq Z$$ }}} Change your function so that it includes the p-value (for a two sided test) as result. * now let the result be a named vector containing the estimated difference, Z, p and the n. |
| Zeile 76: | Zeile 86: |
| == Z-test for a population mean == | === Solutions === |
| Zeile 86: | Zeile 96: |
| == Z-test for a population mean == | |
| Zeile 95: | Zeile 105: |
| == Z-test for a population mean == The function pnorm(Z) gives the probability of {{{#!latex x \leq Z {{{#!latex . Change your function so that it has the p-value (for a two sided test) as result. |
The function pnorm(Z) gives the probability of {{{#!latex $$x \leq Z$$ }}} . Change your function so that it has the p-value (for a two sided test) as result. |
| Zeile 108: | Zeile 120: |
| == Z-test for a population mean == | |
| Zeile 120: | Zeile 132: |
| diff Z pval n }}} == Z-test for a population mean == * Z-test for two population means (variances known and equal) * Z-test for two population means (variances known and unequal) To investigate the statistical significance of the difference between an assumed population mean {{{#!latex \mu_0}}} and a sample mean {{{#!latex \bar{x}}}}. There is a function z.test() in the BSDA package. * It is necessary that the population variance {{{#!latex \sigma^2}}} is known. * The test is accurate if the population is normally distributed. If the population is not normal, the test will still give an approximate guide. |
diff Z pval n 0.1089 1.0889 0.2762 100.0000 }}} === Requirements === * Z-test for two population means (variances known and equal) * Z-test for two population means (variances known and unequal) To investigate the statistical significance of the difference between an assumed population mean {{{#!latex $\mu_0$}}} and a sample mean {{{#!latex $\bar{x}$}}}. There is a function z.test() in the BSDA package * It is necessary that the population variance {{{#!latex $\sigma^2$}}} is known. * The test is accurate if the population is normally distributed. If the population is not normal, the test will still give an approximate guide. |
| Zeile 129: | Zeile 150: |
| * Now sample 100 values from a Normal distribution with mean 10 and standard deviation 2 and use a z-test to compare it against the population mean 10. What is the p-value? * Now do the sampling and the testing 1000 times, what would be the number of statistically significant results? Use replicate() (which is a wrapper of tapply()) or a for() loop! Record at least the p-values and the estimated differences! Use table() to count the p-vals below 0.05. What type of error do you associate with it? What is the smallest absolute difference with a p-value below 0.05? * Repeat the simulation above, change the sample size to 1000 in each of the 1000 samples! How many p-values below 0.05? What is now the smallest absolute difference with a p-value below 0.05? == Simulation Exercises -- Solutions == * Now sample 100 values from a Normal distribution with mean 10 and standard deviation 2 and use a z-test to compare it against the population mean 10. What is the p-value? What the estimated difference? |
* Now sample 100 values from a Normal distribution with mean 10 and standard deviation 2 and use a z-test to compare it against the population mean 10. What is the p-value? * Now do the sampling and the testing 1000 times, what would be the number of statistically significant results? Use replicate() (which is a wrapper of tapply()) or a for() loop! Record at least the p-values and the estimated differences! Use table() to count the p-vals below 0.05. What type of error do you associate with it? What is the smallest absolute difference with a p-value below 0.05? * Repeat the simulation above, change the sample size to 1000 in each of the 1000 samples! How many p-values below 0.05? What is now the smallest absolute difference with a p-value below 0.05? === Simulation Exercises -- Solutions === * Now sample 100 values from a Normal distribution with mean 10 and standard deviation 2 and use a z-test to compare it against the population mean 10. What is the p-value? What the estimated difference? |
| Zeile 136: | Zeile 157: |
| pval | pval 0.0441 |
| Zeile 138: | Zeile 160: |
| diff | diff -0.0655 |
| Zeile 140: | Zeile 163: |
| pval diff }}} == Simulation Exercises -- Solutions == |
pval diff 0.4515 0.1506 }}} |
| Zeile 144: | Zeile 168: |
| using replicate()\footnotesize | === Solution === * using replicate() |
| Zeile 157: | Zeile 183: |
| == Simulation Exercises -- Solutions == * Now do the sampling and the testing 1000 times, what would be the number of statistically significant results? Use replicate() (which is a wrapper of tapply()) or a for() loop. Record at least the p-values and the estimated differences! Transform the result into a data frame. using replicate() II\footnotesize |
* using replicate() II |
| Zeile 168: | Zeile 194: |
| == Simulation Exercises -- Solutions == * Now do the sampling and the testing 1000 times, what would be the number of statistically significant results? Use replicate() (which is a wrapper of tapply()) or a for() loop. Record at least the p-values and the estimated differences! Transform the result into a data frame. using for() \scriptsize |
* using for() |
| Zeile 186: | Zeile 212: |
| == Simulation Exercises -- Solutions == | |
| Zeile 193: | Zeile 219: |
| $`FALSE` Min. 1st Qu. Median Mean 3rd Qu. Max. 0.0002 0.0585 0.1280 0.1411 0.2068 0.3847 $`TRUE` Min. 1st Qu. Median Mean 3rd Qu. Max. 0.3928 0.4247 0.4408 0.4694 0.5102 0.6859 |
|
| Zeile 196: | Zeile 230: |
| == Simulation Exercises -- Solutions == | |
| Zeile 203: | Zeile 237: |
| diff Z pval n | diff Z pval n |
| Zeile 211: | Zeile 245: |
| == Simulation Exercises -- Solutions == | |
| Zeile 218: | Zeile 252: |
| $`FALSE` Min. 1st Qu. Median Mean 3rd Qu. Max. 0.00010 0.02092 0.04285 0.05149 0.07400 0.22610 $`TRUE` Min. 1st Qu. Median Mean 3rd Qu. Max. 0.00240 0.02115 0.04535 0.05435 0.08433 0.14760 |
|
| Zeile 220: | Zeile 261: |
| * Concatenate the both resulting data frames from above using rbind() * Plot the distributions of the pvals and the difference per sample size. Use ggplot2 with an appropriate geom (density/histogram) * What is the message? == Simulation Exercises -- Solutions == |
* Concatenate the both resulting data frames from above using rbind() * Plot the distributions of the pvals and the difference per sample size. Use ggplot2 with an appropriate geom (density/histogram) * What is the message? === Simulation Exercises -- Solutions === |
| Zeile 234: | Zeile 275: |
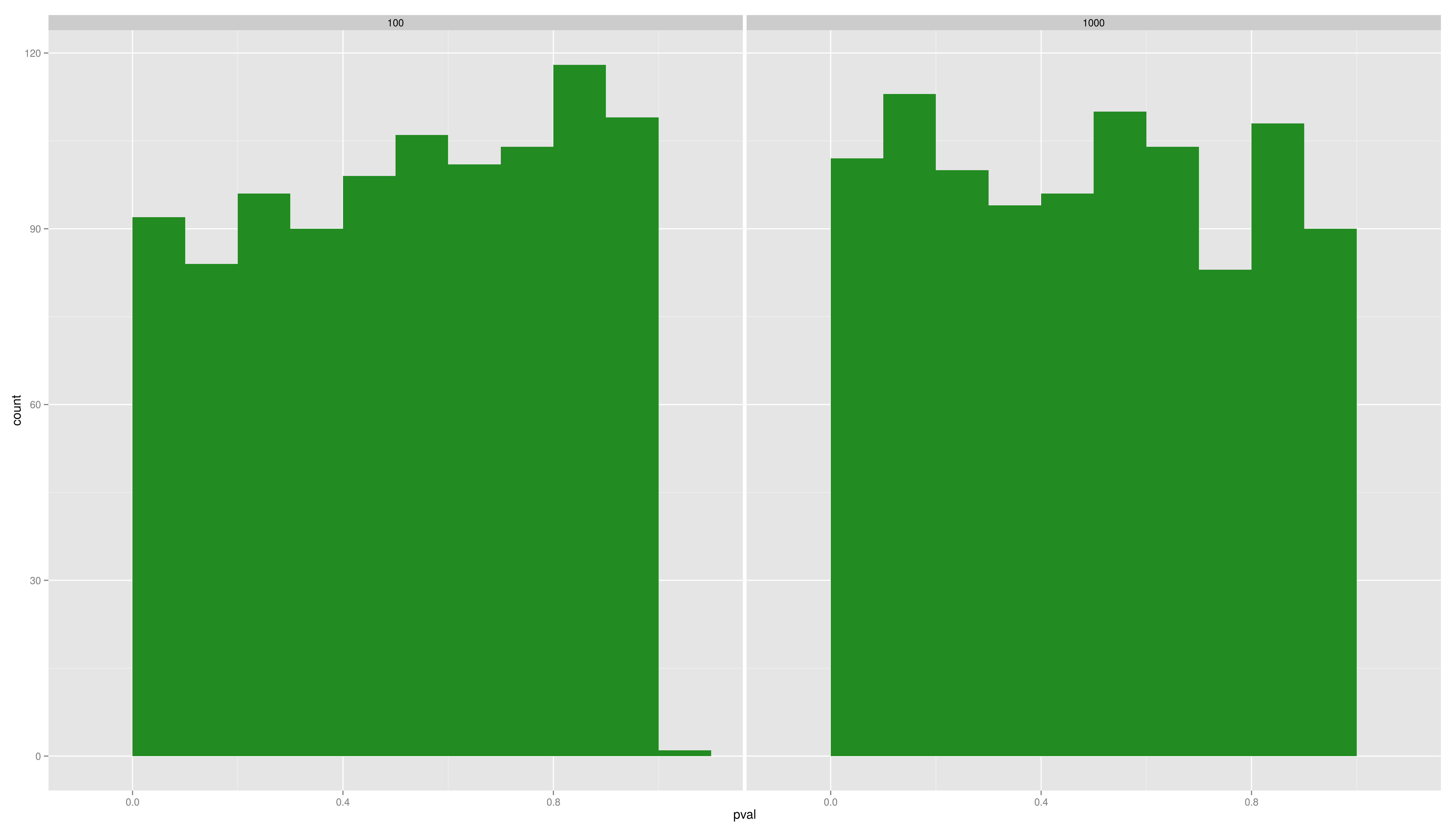
| == Simulation Exercises -- Solutions == <img alt='sesssion2/hist.png' src='-1' /> == Simulation Exercises -- Solutions == |
[[attachment:hist.png|{{attachment:hist.png||width=800}}]] |
| Zeile 244: | Zeile 285: |
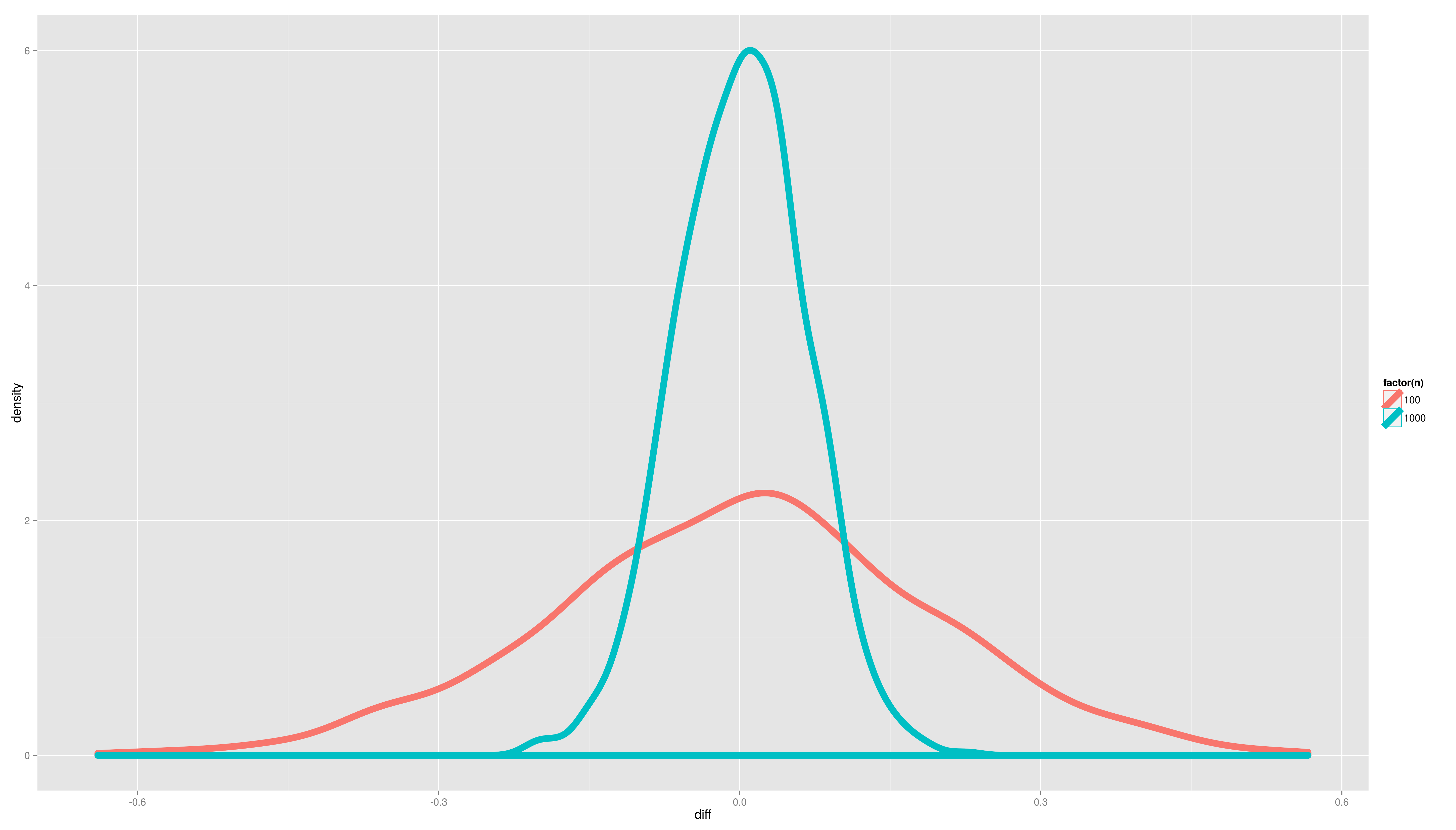
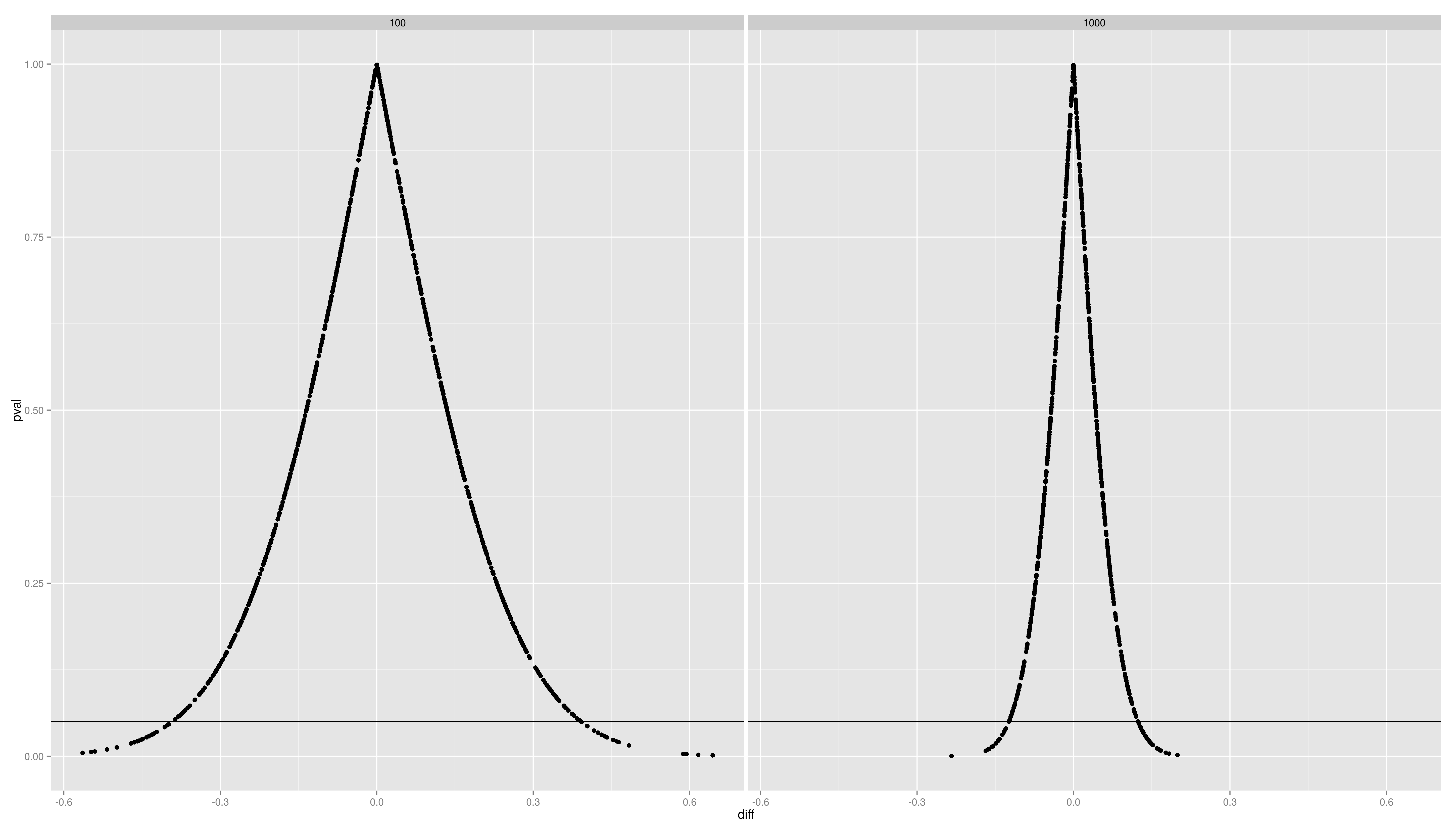
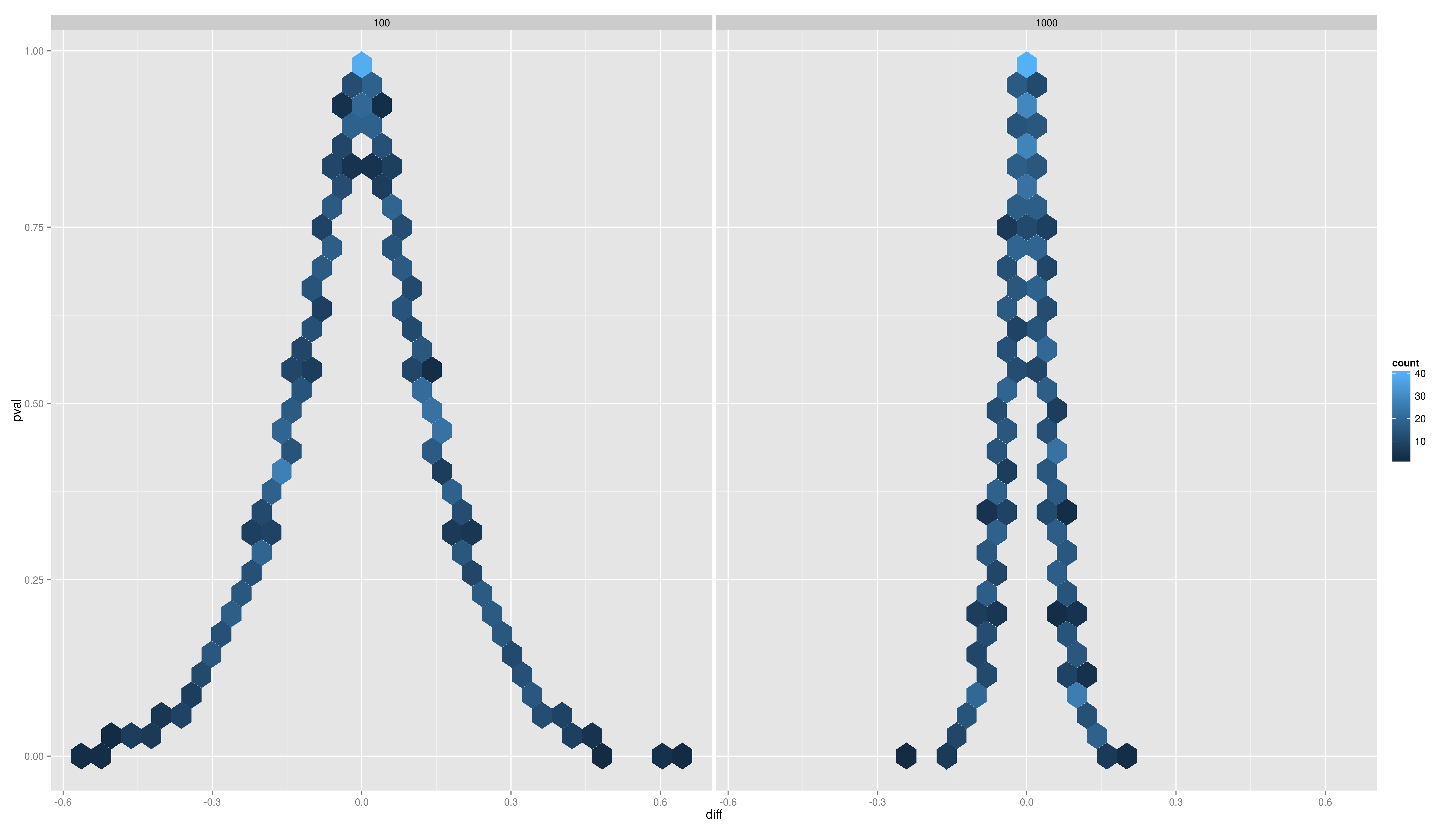
| <img alt='sesssion2/dens.png' src='-1' /> == Simulation Exercises -- Solutions == <img alt='sesssion2/point.png' src='-1' /> == Simulation Exercises -- Solutions == <img alt='sesssion2/dens2d.png' src='-1' /> |
[[attachment:dens.png|{{attachment:dens.png||width=800}}]] [[attachment:point.png|{{attachment:point.png||width=800}}]] [[attachment:dens2d.png|{{attachment:dens2d.png||width=800}}]] == t-tests == A t-test is any statistical hypothesis test in which the test statistic follows a Student's t distribution if the null hypothesis is supported. * one sample t-test: test a sample mean against a population mean {{{#!latex $$t = \frac{\bar{x}-\mu_0}{s/\sqrt{n}}$$ }}} where {{{#!latex $\bar{x}$ }}} is the sample mean, s is the sample standard deviation and n is the sample size. The degrees of freedom used in this test is n-1 === one sample t-test === |
| Zeile 253: | Zeile 310: |
One Sample t-test data: x |
|
| Zeile 256: | Zeile 317: |
| -0.2464740 0.7837494 | |
| Zeile 258: | Zeile 320: |
| }}} {{{#!highlight r |
0.2686377 |
| Zeile 261: | Zeile 323: |
One Sample t-test data: x |
|
| Zeile 264: | Zeile 330: |
| -0.2464740 0.7837494 | |
| Zeile 266: | Zeile 333: |
| }}} == t-tests == A t-test is any statistical hypothesis test in which the test statistic follows a \emph{Student's t distribution} if the null hypothesis is supported. * \emph{one sample t-test}: test a sample mean against a population mean == One Sample t-test == |
0.2686377 }}} |
| Zeile 274: | Zeile 340: |
| * given one vector x containing all the measurement values and one vector g containing the group membership {{{#!latex t.test(x \sim g)}}} (read: x dependend on g) == Two Sample t-tests: two vector syntax == |
* given one vector x containing all the measurement values and one vector g containing the group membership {{{#!latex t.test(x $\sim$ g) }}} (read: x dependend on g) === Two Sample t-tests: two vector syntax === |
| Zeile 282: | Zeile 352: |
| > t.test(x,y) Welch Two Sample t-test data: x and y |
|
| Zeile 285: | Zeile 360: |
| sample estimates: mean of x mean of y }}} == Two Sample t-tests: formula syntax == |
-0.5966988 1.0717822 sample estimates: mean of x mean of y 0.26863768 0.03109602 }}} === Two Sample t-tests: formula syntax === |
| Zeile 291: | Zeile 368: |
Welch Two Sample t-test data: x by g |
|
| Zeile 294: | Zeile 375: |
| -1.6136329 0.9171702 | |
| Zeile 296: | Zeile 378: |
| }}} == Welch/Satterthwaite vs. Student == |
0.1235413 0.4717726 }}} === Welch/Satterthwaite vs. Student === |
| Zeile 303: | Zeile 386: |
Two Sample t-test data: x and y |
|
| Zeile 306: | Zeile 393: |
| sample estimates: mean of x mean of y }}} == t-test == |
-0.5918964 1.0669797 sample estimates: mean of x mean of y 0.26863768 0.03109602 }}} === Requirements === |
| Zeile 311: | Zeile 400: |
| * it is also recommended for group sizes {{{#!latex \geq 30}}} (robust against deviation from normality) | * it is also recommended for group sizes > 30 (robust against deviation from normality) |
| Zeile 313: | Zeile 402: |
| * use a t-test to compare TTime according to Stim.Type, visualize it. What is the problem? * now do the same for Subject 1 on pre and post test (use filter() or indexing to get the resp. subsets) * use the following code to do the test on every subset Subject and testid, try to figure what is happening in each step:\tiny {{{#!highlight r tob <- t.test(x$TTime ~ x$Stim.Type) tmp <- data.frame( Subject = unique(x$Subject), testid = unique(x$testid), pval = tob$p.value, alternative = tob$alternative, |
* use a t-test to compare TTime according to Stim.Type, visualize it. What is the problem? * now do the same for Subject 1 on pre and post test (use filter() or indexing to get the resp. subsets) * use the following code to do the test on every subset Subject and testid, try to figure what is happening in each step:\tiny {{{#!highlight r data.l <- split(data,list(data$Subject,data$testid),drop=T) tmp.l <- lapply(data.l,function(x) { if(min(table(x$Stim.Type)) < 5) return(NULL) tob <- t.test(x$TTime ~ x$Stim.Type) tmp <- data.frame( Subject = unique(x$Subject), testid = unique(x$testid), mean.group.1 = tob$estimate[1], mean.group.2 = tob$estimate[2], name.test.stat = tob$statistic, conf.lower = tob$conf.int[1], conf.upper = tob$conf.int[2], pval = tob$p.value, alternative = tob$alternative, tob$method)}) |
| Zeile 325: | Zeile 424: |
| * make plots to visualize the results. * how many tests have a statistically significant result? How many did you expect? Is there a tendency? What could be the next step? == Exercises - Solutions == |
* make plots to visualize the results. * how many tests have a statistically significant result? How many did you expect? Is there a tendency? What could be the next step? === Solutions === |
| Zeile 331: | Zeile 430: |
Welch Two Sample t-test data: data$TTime by data$Stim.Type |
|
| Zeile 334: | Zeile 437: |
| sample estimates: mean in group hit mean in group incorrect |
-2773.574 -1466.161 sample estimates: mean in group hit mean in group incorrect 17579.77 19699.64 |
| Zeile 339: | Zeile 445: |
| == Exercises - Solutions == | |
| Zeile 344: | Zeile 449: |
Welch Two Sample t-test data: data$TTime[data$Subject == 1 & data$testid == "test1"] by data$Stim.Type[data$Subject == 1 & data$testid == "test1"] |
|
| Zeile 347: | Zeile 456: |
| sample estimates: mean in group hit mean in group incorrect |
-4930.842 2713.191 sample estimates: mean in group hit mean in group incorrect 8248.175 9357.000 |
| Zeile 351: | Zeile 464: |
| Welch Two Sample t-test data: data$TTime[data$Subject == 1 & data$testid == "test2"] by data$Stim.Type[data$Subject == 1 & data$testid == "test2"] |
|
| Zeile 354: | Zeile 470: |
| sample estimates: mean in group hit mean in group incorrect }}} == Exercises - Solutions == |
-7004.4904 448.9388 sample estimates: mean in group hit mean in group incorrect 4012.480 7290.256 }}} |
| Zeile 367: | Zeile 484: |
| == Exercises - Solutions == | |
| Zeile 374: | Zeile 490: |
| FALSE TRUE | FALSE TRUE 0.8823529 0.1176471 |
| Zeile 380: | Zeile 498: |
| tob <- t.test(x$TTime ~ x$Stim.Type) tmp <- data.frame( Subject = unique(x$Subject), testid = unique(x$testid), pval = tob$p.value, alternative = tob$alternative, |
tmp.l <- lapply(data.l,function(x) { if(min(table(x$Stim.Type)) < 5) return(NULL) tob <- t.test(x$TTime ~ x$Stim.Type) tmp <- data.frame( Subject = unique(x$Subject), testid = unique(x$testid), perc.corr = sum(x$Stim.Type=="hit")/sum(!is.na(x$Stim.Type)), mean.group.1 = tob$estimate[1], mean.group.2 = tob$estimate[2], name.test.stat = tob$statistic, conf.lower = tob$conf.int[1], conf.upper = tob$conf.int[2], pval = tob$p.value, alternative = tob$alternative, tob$method)}) |
| Zeile 387: | Zeile 515: |
| }}} | ggplot(res,aes(x=perc.corr,y=mean.group.1 - mean.group.2)) + geom_point() + geom_smooth() }}} [[attachment:excerchypo.pdf|{{attachment:exerchypo.pdf||width=800,height=400}}]] |
Classical Tests
Exercises
- load the data (file: session4data.rdata)
- make a new summary data frame (per subject and time) containing:
- the number of trials
- the number correct trials (absolute and relative)
- the mean TTime and the standard deviation of TTime
- the respective standard error of the mean
- keep the information about Sex and Age_PRETEST
- make a plot with time on the x-axis and TTime on the y-axis showing the means and the 95\% confidence intervals (geom_pointrange())
- add the number of trials and the percentage of correct ones using geom_text()
Exercises - Solutions
- load the data (file: session4data.rdata)
- make a new summary data frame (per subject and time) containing:
1 > sumdf <- data %>%
2 + group_by(Subject,Sex,Age_PRETEST,testid) %>%
3 + summarise(count=n(),
4 + n.corr = sum(Stim.Type=="hit"),
5 + perc.corr = n.corr/count,
6 + mean.ttime = mean(TTime),
7 + sd.ttime = sd(TTime),
8 + se.ttime = sd.ttime/sqrt(count))
9 > head(sumdf)
10 Subject Sex Age_PRETEST testid count n.corr perc.corr mean.ttime
11 1 1 f 3.11 test1 95 63 0.6631579 8621.674
12 2 1 f 3.11 1 60 32 0.5333333 9256.367
13 3 1 f 3.11 2 59 32 0.5423729 9704.712
14 4 1 f 3.11 3 60 38 0.6333333 14189.550
15 5 1 f 3.11 4 59 31 0.5254237 13049.831
16 6 1 f 3.11 5 59 33 0.5593220 14673.525
17 Variables not shown: sd.ttime se.ttime (dbl)
four possible situations
|
Situation |
||
|
H_0 is true |
H_0 is false |
|
Conclusion |
H_0 is not rejected |
Correct decision |
Type II error |
H_0 is rejected |
Type I error |
Correct decision |
|
Common symbols
n |
number of observations (sample size) |
K |
number of samples (each having n elements) |
alpha |
level of significance |
nu |
degrees of freedom |
mu |
population mean |
xbar |
sample mean |
sigma |
standard deviation (population) |
s |
standard deviation (sample) |
rho |
population correlation coefficient |
r |
sample correlation coefficient |
Z |
standard normal deviate |
Alternatives
The p-value is the probability of the sample estimate (of the respective estimator) under the null. The p-value is NOT the probability that the null is true.
Z-test for a population mean
The z-test is a something like a t-test (it is like you would know almost everything about the perfect conditions. It uses the normal distribution as distribution of the test statistic and is therefore a good example.
- To investigate the significance of the difference between an assumed population mean
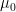
and a sample mean
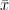
It is necessary that the population variance
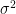
is known.
- The test is accurate if the population values are normally distributed. If the population values are not normal, the test will still give an approximate guide.
Excercise
- Write a function which takes a vector, the population standard deviation and the population mean as arguments and which gives the Z score as result.
- name the function ztest or my.z.test - not z.test because z.test is already used
- set a default value for the population mean
- add a line to your function that allows you to process numeric vectors containing missing values!
- the function pnorm(Z) gives the probability of
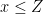
Change your function so that it includes the p-value (for a two sided test) as result.
- now let the result be a named vector containing the estimated difference, Z, p and the n.
You can always test your function using simulated values: rnorm(100,mean=0) gives you a vector containing 100 normal distributed values with mean 0.
Solutions
Write a function which takes a vector, the population standard deviation and the population mean as arguments and which gives the Z score as result.
Add a line to your function that allows you to also process numeric vectors containing missing values!
The function pnorm(Z) gives the probability of
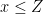
. Change your function so that it has the p-value (for a two sided test) as result.
Now let the result be a named vector containing the estimated difference, Z, p and the n.
1 > ztest <- function(x,x.sd,mu=0){
2 + x <- x[!is.na(x)]
3 + if(length(x) < 3) stop("too few values in x")
4 + est.diff <- mean(x)-mu
5 + z <- sqrt(length(x)) * (est.diff)/x.sd
6 + round(c(diff=est.diff,Z=z,pval=2*pnorm(-abs(z)),n=length(x)),4)
7 + }
8 > set.seed(1)
9 > ztest(rnorm(100),x.sd = 1)
10 diff Z pval n
11 0.1089 1.0889 0.2762 100.0000
Requirements
- Z-test for two population means (variances known and equal)
- Z-test for two population means (variances known and unequal)
To investigate the statistical significance of the difference between an assumed population mean
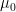
and a sample mean
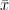
. There is a function z.test() in the BSDA package
- It is necessary that the population variance
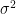
is known.
- The test is accurate if the population is normally distributed. If the population is not normal, the test will still give an approximate guide.
Simulation Exercises
- Now sample 100 values from a Normal distribution with mean 10 and standard deviation 2 and use a z-test to compare it against the population mean 10. What is the p-value?
- Now do the sampling and the testing 1000 times, what would be the number of statistically significant results? Use replicate() (which is a wrapper of tapply()) or a for() loop! Record at least the p-values and the estimated differences! Use table() to count the p-vals below 0.05. What type of error do you associate with it? What is the smallest absolute difference with a p-value below 0.05?
- Repeat the simulation above, change the sample size to 1000 in each of the 1000 samples! How many p-values below 0.05? What is now the smallest absolute difference with a p-value below 0.05?
Simulation Exercises -- Solutions
- Now sample 100 values from a Normal distribution with mean 10 and standard deviation 2 and use a z-test to compare it against the population mean 10. What is the p-value? What the estimated difference?
- Now do the sampling and the testing 1000 times, what would be the number of statistically significant results? Use replicate() (which is a wrapper of tapply()) or a for() loop. Record at least the p-values and the estimated differences! Transform the result into a data frame.
Solution
- using replicate()
1 > res <- replicate(1000, ztest(rnorm(100,mean=10,sd=2),x.sd=2,mu=10))
2 > res <- as.data.frame(t(res))
3 > head(res)
4 diff Z pval n
5 1 -0.2834 -1.4170 0.1565 100
6 2 0.2540 1.2698 0.2042 100
7 3 -0.1915 -0.9576 0.3383 100
8 4 0.1462 0.7312 0.4646 100
9 5 0.1122 0.5612 0.5747 100
10 6 -0.0141 -0.0706 0.9437 100
- using replicate() II
- using for()
1 > res <- matrix(numeric(2000),ncol=2)
2 > for(i in seq.int(1000)){
3 + res[i,] <- ztest(rnorm(100,mean=10,sd=2),x.sd=2,mu=10)[c("pval","diff")] }
4 > res <- as.data.frame(res)
5 > names(res) <- c("pval","diff")
6 > head(res)
7 pval diff
8 1 0.0591 -0.3775
9 2 0.2466 0.2317
10 3 0.6368 0.0944
11 4 0.5538 -0.1184
12 5 0.9897 -0.0026
13 6 0.7748 0.0572
- Use table() to count the p-vals below 0.05. What type of error do you associate with it? What is the smallest absolute difference with a p-value below 0.05?
1 > table(res$pval < 0.05)
2 FALSE TRUE
3 960 40
4 > tapply(abs(res$diff),res$pval < 0.05,summary)
5 $`FALSE`
6 Min. 1st Qu. Median Mean 3rd Qu. Max.
7 0.0002 0.0585 0.1280 0.1411 0.2068 0.3847
8
9 $`TRUE`
10 Min. 1st Qu. Median Mean 3rd Qu. Max.
11 0.3928 0.4247 0.4408 0.4694 0.5102 0.6859
12
13 > min(abs(res$diff[res$pval<0.05]))
14 [1] 0.3928
- Repeat the simulation above, change the sample size to 1000 in each of the 1000 samples! How many p-values below 0.05? What is now the smallest absolute difference with a p-value below 0.05?
1 > res2 <- replicate(1000, ztest(rnorm(1000,mean=10,sd=2),
2 + x.sd=2,mu=10))
3 > res2 <- as.data.frame(t(res2))
4 > head(res2)
5 diff Z pval n
6 1 -0.0731 -1.1559 0.2477 1000
7 2 0.0018 0.0292 0.9767 1000
8 3 0.0072 0.1144 0.9089 1000
9 4 -0.1145 -1.8100 0.0703 1000
10 5 -0.1719 -2.7183 0.0066 1000
11 6 0.0880 1.3916 0.1640 1000
- Repeat the simulation above, change the sample size to 1000 in each of the 1000 samples! How many p-values below 0.05? What is now the smallest absolute difference with a p-value below 0.05?
1 > table(res2$pval < 0.05)
2 FALSE TRUE
3 946 54
4 > tapply(abs(res2$diff),res$pval < 0.05,summary)
5 $`FALSE`
6 Min. 1st Qu. Median Mean 3rd Qu. Max.
7 0.00010 0.02092 0.04285 0.05149 0.07400 0.22610
8
9 $`TRUE`
10 Min. 1st Qu. Median Mean 3rd Qu. Max.
11 0.00240 0.02115 0.04535 0.05435 0.08433 0.14760
Simulation Exercises Part II
- Concatenate the both resulting data frames from above using rbind()
- Plot the distributions of the pvals and the difference per sample size. Use ggplot2 with an appropriate geom (density/histogram)
- What is the message?
Simulation Exercises -- Solutions
- Concatenate the both resulting data frames from above using rbind()
- Plot the distributions of the pvals and the difference per sample size. Use ggplot2 with an appropriate geom (density/histogram)
- Plot the distributions of the pvals and the difference per sample size. Use ggplot2 with an appropriate geom (density/histogram)
Simulation Exercises -- Solutions
t-tests
A t-test is any statistical hypothesis test in which the test statistic follows a Student's t distribution if the null hypothesis is supported.
- one sample t-test: test a sample mean against a population mean

where
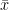
is the sample mean, s is the sample standard deviation and n is the sample size. The degrees of freedom used in this test is n-1
one sample t-test
1 > set.seed(1)
2 > x <- rnorm(12)
3 > t.test(x,mu=0) ## population mean 0
4
5 One Sample t-test
6
7 data: x
8 t = 1.1478, df = 11, p-value = 0.2754
9 alternative hypothesis: true mean is not equal to 0
10 95 percent confidence interval:
11 -0.2464740 0.7837494
12 sample estimates:
13 mean of x
14 0.2686377
15
16 > t.test(x,mu=1) ## population mean 1
17
18 One Sample t-test
19
20 data: x
21 t = -3.125, df = 11, p-value = 0.009664
22 alternative hypothesis: true mean is not equal to 1
23 95 percent confidence interval:
24 -0.2464740 0.7837494
25 sample estimates:
26 mean of x
27 0.2686377
Two Sample t-tests
There are two ways to perform a two sample t-test in R:
- given two vectors x and y containing the measurement values from the respective groups t.test(x,y)
- given one vector x containing all the measurement values and one vector g containing the group membership
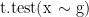
(read: x dependend on g)
Two Sample t-tests: two vector syntax
1 > set.seed(1)
2 > x <- rnorm(12)
3 > y <- rnorm(12)
4 > g <- sample(c("A","B"),12,replace = T)
5 > t.test(x,y)
6 > t.test(x,y)
7
8 Welch Two Sample t-test
9
10 data: x and y
11 t = 0.5939, df = 20.012, p-value = 0.5592
12 alternative hypothesis: true difference in means is not equal to 0
13 95 percent confidence interval:
14 -0.5966988 1.0717822
15 sample estimates:
16 mean of x mean of y
17 0.26863768 0.03109602
Two Sample t-tests: formula syntax
1 > t.test(x ~ g)
2
3 Welch Two Sample t-test
4
5 data: x by g
6 t = -0.6644, df = 6.352, p-value = 0.5298
7 alternative hypothesis: true difference in means is not equal to 0
8 95 percent confidence interval:
9 -1.6136329 0.9171702
10 sample estimates:
11 mean in group A mean in group B
12 0.1235413 0.4717726
Welch/Satterthwaite vs. Student
- if not stated otherwise t.test() will not assume that the variances in the both groups are equal
- if one knows that both populations have the same variance set the var.equal argument to TRUE to perform a student's t-test
Student's t-test
1 > t.test(x, y, var.equal = T)
2
3 Two Sample t-test
4
5 data: x and y
6 t = 0.5939, df = 22, p-value = 0.5586
7 alternative hypothesis: true difference in means is not equal to 0
8 95 percent confidence interval:
9 -0.5918964 1.0669797
10 sample estimates:
11 mean of x mean of y
12 0.26863768 0.03109602
Requirements
- the t-test, especially the Welch test is appropriate whenever the values are normally distributed
it is also recommended for group sizes > 30 (robust against deviation from normality)
Exercises
- use a t-test to compare TTime according to Stim.Type, visualize it. What is the problem?
- now do the same for Subject 1 on pre and post test (use filter() or indexing to get the resp. subsets)
- use the following code to do the test on every subset Subject and testid, try to figure what is happening in each step:\tiny
1 data.l <- split(data,list(data$Subject,data$testid),drop=T)
2 tmp.l <- lapply(data.l,function(x) {
3 if(min(table(x$Stim.Type)) < 5) return(NULL)
4 tob <- t.test(x$TTime ~ x$Stim.Type)
5 tmp <- data.frame(
6 Subject = unique(x$Subject),
7 testid = unique(x$testid),
8 mean.group.1 = tob$estimate[1],
9 mean.group.2 = tob$estimate[2],
10 name.test.stat = tob$statistic,
11 conf.lower = tob$conf.int[1],
12 conf.upper = tob$conf.int[2],
13 pval = tob$p.value,
14 alternative = tob$alternative,
15 tob$method)})
16 res <- Reduce(rbind,tmp.l)
- make plots to visualize the results.
- how many tests have a statistically significant result? How many did you expect? Is there a tendency? What could be the next step?
Solutions
- use a t-test to compare TTime according to Stim.Type, visualize it. What is the problem?
1 > t.test(data$TTime ~ data$Stim.Type)
2
3 Welch Two Sample t-test
4
5 data: data$TTime by data$Stim.Type
6 t = -6.3567, df = 9541.891, p-value = 2.156e-10
7 alternative hypothesis: true difference in means is not equal to 0
8 95 percent confidence interval:
9 -2773.574 -1466.161
10 sample estimates:
11 mean in group hit mean in group incorrect
12 17579.77 19699.64
13
14 > ggplot(data,aes(x=Stim.Type,y=TTime)) +
15 + geom_boxplot()
- now do the same for Subject 1 on pre and post test (use filter() or indexing to get the resp. subsets)
1 > t.test(data$TTime[data$Subject==1 & data$testid=="test1"] ~
2 + data$Stim.Type[data$Subject==1 & data$testid=="test1"])
3
4 Welch Two Sample t-test
5
6 data: data$TTime[data$Subject == 1 & data$testid == "test1"] by data$Stim.Type[data$Subject == 1 & data$testid == "test1"]
7 t = -0.5846, df = 44.183, p-value = 0.5618
8 alternative hypothesis: true difference in means is not equal to 0
9 95 percent confidence interval:
10 -4930.842 2713.191
11
12 sample estimates:
13 mean in group hit mean in group incorrect
14 8248.175 9357.000
15
16 > t.test(data$TTime[data$Subject==1 & data$testid=="test2"] ~
17 + data$Stim.Type[data$Subject==1 & data$testid=="test2"])
18 Welch Two Sample t-test
19
20 data: data$TTime[data$Subject == 1 & data$testid == "test2"] by data$Stim.Type[data$Subject == 1 & data$testid == "test2"]
21 t = -1.7694, df = 47.022, p-value = 0.08332
22 alternative hypothesis: true difference in means is not equal to 0
23 95 percent confidence interval:
24 -7004.4904 448.9388
25 sample estimates:
26 mean in group hit mean in group incorrect
27 4012.480 7290.256
- make plots to visualize the results
- how many tests have an statistically significant result? How many did you expect?
Exercises - Solutions
- What could be the next step?
1 tmp.l <- lapply(data.l,function(x) {
2 if(min(table(x$Stim.Type)) < 5) return(NULL)
3 tob <- t.test(x$TTime ~ x$Stim.Type)
4 tmp <- data.frame(
5 Subject = unique(x$Subject),
6 testid = unique(x$testid),
7 perc.corr = sum(x$Stim.Type=="hit")/sum(!is.na(x$Stim.Type)),
8 mean.group.1 = tob$estimate[1],
9 mean.group.2 = tob$estimate[2],
10 name.test.stat = tob$statistic,
11 conf.lower = tob$conf.int[1],
12 conf.upper = tob$conf.int[2],
13 pval = tob$p.value,
14 alternative = tob$alternative,
15 tob$method)})
16
17 res <- Reduce(rbind,tmp.l)
18
19 ggplot(res,aes(x=perc.corr,y=mean.group.1 - mean.group.2)) +
20 geom_point() +
21 geom_smooth()